Aufgabe
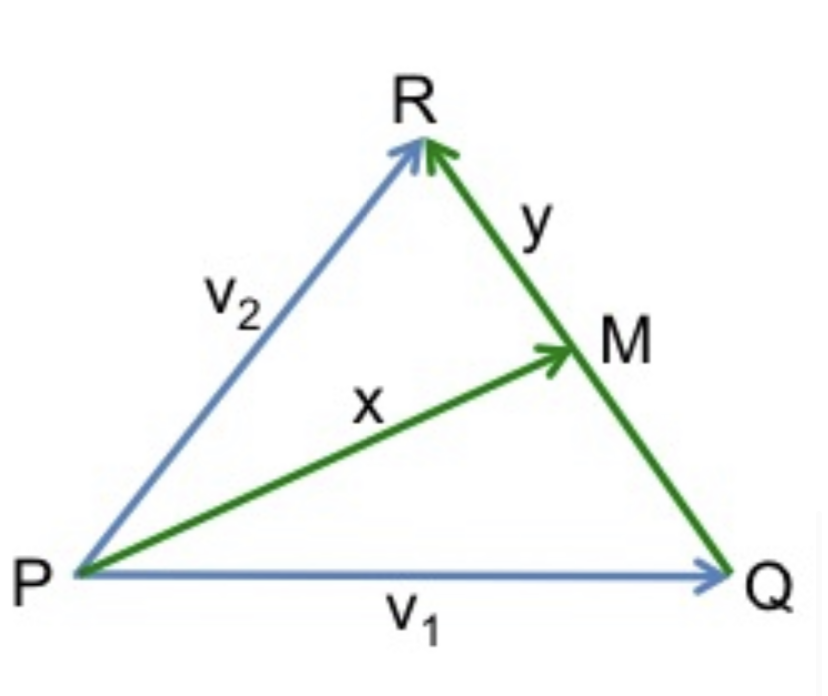
Das Dreieck P QR ist festgelegt durch die Vektoren v1 = P Q und v2 = P R. Der Mittelpunkt der Seite QR sei M (s. Skizze).
Wir betrachten die Menge E aller Linearkombinationen der Vektorenv1 undv2;d.h.E={λ1v1+λ2v2 |λ1,λ2 ∈R}.
−→ −→
Zeigen Sie:
(i) Die Vektoren x = PM und y = QR liegen in der Menge E.
(ii) x und y sind linear unabhängig
(iii) Stellen Sie u = \( \frac{3}{2} \) v1− 2 v2 als Linearkombination von x und
y dar.
(b) Es seien a,b1,...,bn,c∈Rn.
Zeigen Sie, dass aus a∈span(b1,...,bn,c) und a∉span(b1,...,bn)
gefolgert werden kann:
c ∈ span(a,b1,...,bn)
Problem/Ansatz:
Ich habe diese Aufgabe in meinem Übungsblatt und kann diese als einzige Aufgabe nicht berechnen.
Ich möchte deshalb nicht unter der Mindestpunktzahl liegen.
Könnte mir jemand helfen.