Bestimmen die Parabelgleichung

Question

Aufgabe:

a) Eine Parabel schneidet die x-Achse in N1(-2/0) und N2 (4/0).Ihr Scheitel ist (Xs/-6).

b)Eine Parabel schneidet die x-Achse in N1(3/0) und hat den Scheitel S(1/2).

c)Eine Parabel schneidet die Achsen in N1(-3/0),N2(5/0) und P(0/6).

Problem/Ansatz:

Wäre nett, wenn mir jemand helfen könnte:)

Answer 1

a) Eine Parabel schneidet die x-Achse in N1(-2|0) und N2 (4|0).Ihr Scheitel ist (x S|-6).

f(x)=a*(x+2)*(x-4)

Der Scheitel liegt "in der Mitte" der beiden Nullstellen:

S(1|-6)

f(1)=a*(1+2)*(1-4)=-9a

-9a=-6

a=\( \frac{2}{3} \)

f(x)=\( \frac{2}{3} \)*(x+2)*(x-4)

Answer 2

Hallo,

es gibt prinzipiell drei Rechenwege, um eine Parabelgleichung zu bestimmen.

1) Drei Punkte sind gegeben.

f(x)=ax^2+bx+c

Die Koordinaten der Punkte einsetzen, a, b und c ausrechnen.

2) Beide Nullstellen sind gegeben.

y=a(x-x₁)(x-x₂)

Außerdem muss noch eine weitere Information gegeben sein, um a zu bestimmen.

3) Der Scheitelpunkt S(d|e) ist gegeben.

y=a(x-d)^2+e

Auch hier muss noch eine weitere Eigenschaft gegeben sein.

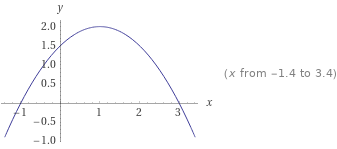
b)Eine Parabel schneidet die x-Achse in N1(3/0) und hat den Scheitel S(1/2).

--> 3)

y=a(x-1)^2+2

Nullstelle --> 0=a(3-1)^2+2 → a=-0,5

y=-0,5(x^2-2x+1)+2

y=-0,5x^2+x+1,5

:-)