Text erkannt:
Der HIV-Test ist einer der zuverlässigsten Tests, die jemals entwickelt wurden. Er wird eingesetzt, um eine Infektion mit HIV festzustellen. Wegen der hohen Gefahr der Verbreitung der tödlichen HIV-
Infektion war sogar lange Zeit ein sogenanntes Massenscreening in der Diskussion, bei dem die gesamte Bevölkerung zum Test gezwungen werden soll. Der HIV-Test ist aber nicht perfekt. Wenn jemand HIV-infiziert ist, soll der Test positiv sein. Zu \( 99,9 \% \) fällt er dann auch positiv aus
(Sensitivität). Andererseits, wenn jemand nicht HIV-infiziert ist, soll der Test natürlich negativ sein. Zu \( 99,7 \% \) fällt er dann tatsächlich negativ aus (Spezifität) \( ^{1} \)
Angenommen für alle Menschen in NRW soll ein HIV-Test durchgeführt werden. Laut Schätzung des Robert-Koch-Instituts sind bundesweit \( 0,1 \%^{2} \) der Bevölkerung HIV-infiziert (Prävalenz), die Quote kann auch für NRW angenommen werden. Die Bevölkerungsstatistik sagt, dass in NRW ca.
\( 18.000 .000 \) Menschen leben.
\( \mathrm{KaDiS} \) to \( 5: \)
5) http://www,rki.de/DE/Content/InfAZ/H/HIVAIDS/Epio Daten und Berichte/EckdatenDeutschland.pdf? \( \quad \) blob=publicationFile
Aufgaben:
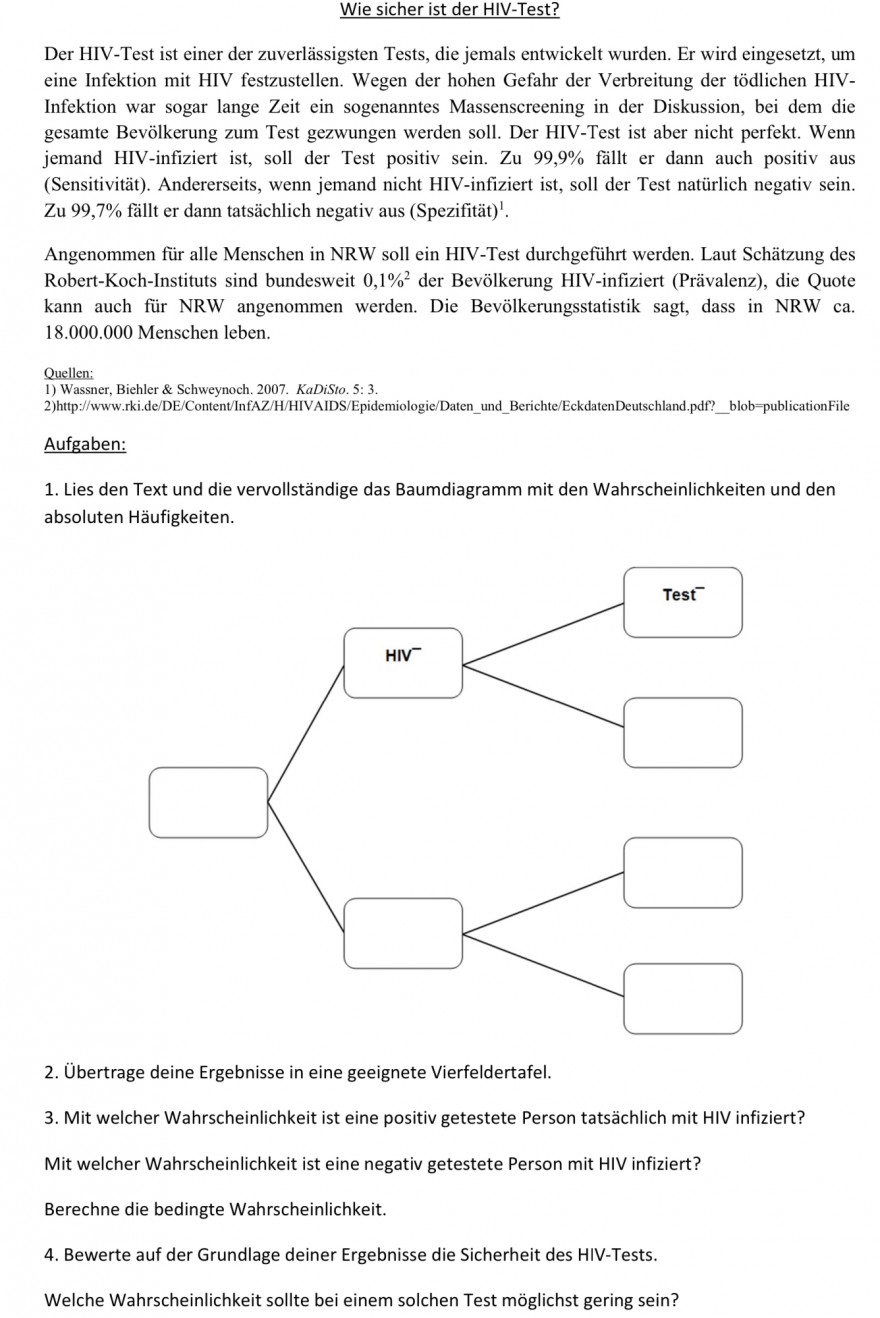
1. Lies den Text und die vervollständige das Baumdiagramm mit den Wahrscheinlichkeiten und den
absoluten Häufigkeiten.
2. Übertrage deine Ergebnisse in eine geeignete Vierfeldertafel.
3. Mit welcher Wahrscheinlichkeit ist eine positiv getestete Person tatsächlich mit HIV infiziert?
Mit welcher Wahrscheinlichkeit ist eine negativ getestete Person mit HIV infiziert?
Berechne die bedingte Wahrscheinlichkeit.
4. Bewerte auf der Grundlage deiner Ergebnisse die Sicherheit des HIV-Tests.
Welche Wahrscheinlichkeit sollte bei einem solchen Test möglichst gering sein?
Text erkannt:
1
Wie sicher ist der HIV-Test?
Der HIV-Test ist einer der zuverlässigsten Tests, die jemals entwickelt wurden. Er wird eingesetzt, um eine Infektion mit HIV festzustellen. Wegen der hohen Gefahr der Verbreitung der tödlichen HIV-
Infektion war sogar lange Zeit ein sogenanntes Massenscreening in der Diskussion, bei dem die gesamte Bevölkerung zum Test gezwungen werden soll. Der HIV-Test ist aber nicht perfekt. Wenn jemand HIV-infiziert ist, soll der Test positiv sein. Zu \( 99,9 \% \) fällt er dann auch positiv aus
(Sensitivität). Andererseits, wenn jemand nicht HIV-infiziert ist, soll der Test natürlich negativ sein
Zu \( 99,7 \% \) fällt er dann tatsächlich negativ aus (Spezifität)
Angenommen für alle Menschen in NRW soll ein HIV-Test durchgeführt werden. Laut Schätzung des Robert-Koch-Instituts sind bundesweit \( 0,1 \%^{2} \) der Bevölkerung HIV-infiziert (Prävalenz), die Quote kann auch für NRW angenommen werden. Die Bevölkerungsstatistik sagt, dass in NRW ca \( 18.000 .000 \) Menschen leben
Bichler \& Schweynoch 20
un \( \mathrm{h} \)
Aufgaben:
1. Lies den Text und die vervollständige das Baumdiagramm mit den Wahrscheinlichkeiten und den
absoluten Häufigkeiten.
2. Übertrage deine Ergebnisse in eine geeignete Vierfeldertafel
3. Mit welcher Wahrscheinlichkeit ist eine positiv getestete Person tatsächlich mit HIV infiziert?
Mit welcher Wahrscheinlichkeit ist eine negativ getestete Person mit HIV infiziert?
Berechne die bedingte Wahrscheinlichkeit.
4. Bewerte auf der Grundlage deiner Ergebnisse die Sicherheit des HIV-Tests.
Welche Wahrscheinlichkeit sollte bei einem solchen Test möglichst gering sein?