Aufgabe:
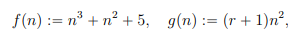
Bitte beachten, dass hier r = 4 ist.
Problem/Ansatz:
Kann mir hier jemand schnell weiterhelfen? Ich weiß, dass ich hier zeigen muss, dass folgendes gilt:
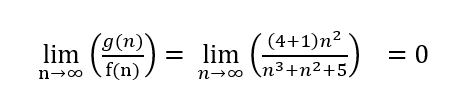
Ist mein Ansatz so richtig?
(i) (4+1)n^2 / n^3 + n^2 + 5
(ii) 5n^2 / n^3 + n^2 + 5
(iii) (n^2 * 5) / n^3 / (1 + (n^2 / n^3) + 5/n^3)
(vi) ((1 * 5) / n) / (1 + (1 / n) + 5/n)
(v) (5 /n) / (1 + (1 / n) + 5/n)
(vi) 1 / (1 + (1 / n) = 1 / 1 + 0 = 1 / 1 = 1
Somit gilt die Aussage NICHT
Falls es falsch ist, kann mir jemand bitte die Lösung richtig stellen, damit ich es dann besser nachvollziehen kann, wo denn hier der Fehler liegt, dafür bekommt ihr von mir ewige Dankbarkeit geschenkt. (︶^︶)