Volumenberechnung eines 8 eckigen Dachstocks

Question

Hallo an alle...

ich möchte gerne das Volumen eines Teils, eines Dachstocks berechnen und weiß nicht, wie ich das bewerkstelligen soll.

Ich habe eine 8 eckige Grundfläche als Dachgeschoss. Die Spitze in der Mitte ist 4m hoch. Jede Aussenkante ist 5m lang. Mittig gemessen von der Aussenkante zur Mitte sin genau 6m.

Wie berechne ich das Volumens eines der 8 Teilkörper (ich nenne sie mal Dreiecke, weil sie von oben betrachtet so aussehen wie ein Dreieck, auch wenn sie es geometrisch nicht sind)

Ich schaffe es nicht. Vielen Dank!

https://www.matheretter.de/rechner/geozeichner?draw=linienzug(-2.5%7C6%202.5%7C6%202.5%7C6%206%7C2.5%206%7C2.5%206%7C-2.5%202.5%7C-6%20-2.5%7C-6%20-6%7C-2.5%20-6%7C2.5%20-2.5%7C6%202.5%7C-6)%0A%0Alinienzug(2.5%7C6%20-2.5%7C-6%20%E2%80%A6)%0A%0Alinienzug(6%7C2.5%20-6%7C-2.5%20%E2%80%A6)%0A%0A%0Alinienzug(-6%7C2.5%206%7C-2.5%20%E2%80%A6)&scale=10

Answer 1

Der Inhalt der achteckigen Grundfläche ist laut Formelsammlung:

A = 8 * 6² * tan 22,5°

und das Volumen des Dachstocks somit

V = \( \int\limits_{0}^{4} \) 8 * (6*x/4)² * tan 22,5° dx ≈ 159

Comments

Vielen Dank für die Antwort.

Ich verstehe diese Rechnung leider nicht. Ich bin Schüler einer 8ten Klasse. Jetzt habe ich 2 Antworten mit, so sieht es für mich aus, zwei unterschiedlichen Ergebnissen. Wären Sie so nett, und könnten mir das ein wenig aufdröseln, sodass ich die Rechnung nachvollziehen kann. Ich wäre Ihnen sehr dankbar.

---

Aufdröseln sollte man die Aufgabenstellung.

Entweder ist eine Aussenkante 4,971 m lang und nicht 5 m, dann ist der Innkreisradius wie in der Aufgabe angegeben 6 m lang. Oder die Aussenkante ist 5 m lang, dann ist der Innkreisradius 6,036 m. Beides miteinander so wie in der Aufgabe angegeben, geht nicht.

---

Ich bedanke mich für die Antwort.

Mit dem Geodreieck sind die 0,36m im Innenkreisradius bzw. die 0,29m der im Maßstab 1:50 in meiner Zeichnung nicht ablesbar. Da liegt der Fehler in der genauen Maßangabe dann eindeutig bei mir. Ich verstehe den Rechenweg zwar trotzdem nicht, weil ich noch nicht einmal das Zeichen (\( \int\limits_{0}^{4} \)) kenne, weil es mir noch niemand bisher in der Schule beigebracht hat, aber freue mich trotzdem darüber, dass Sie mir geholfen haben.

Die 159m³ muss ich jetzt nur noch durch 8 teilen, um ein 1/8 des Dachvolumens zu erhalten. Das ist doch richtig, oder?

Vielen Dank

---

Nein, denn meine Antwort ist falsch. Ich habe 6 m verwendet, wie in der ursprünglichen Aufgabenstellung angegeben. Im in der Zwischenzeit an einem anderen Ort angegebenen Originaltext ist von 6 m nicht die Rede. Ich werde also demnächst eine andere Antwort einstellen, mit einem Rechenweg der für die 8. Klasse eher passen sollte.

---

Ich bedanke micht bereits jetzt schon dafür. ☺

---

Das gesuchte Achtel des Dachstocks ist eine Pyramide. Das Volumen aller Pyramiden, auch wenn sie nicht eine quadratische Grundfläche haben und auch wenn die Spitze nicht über der Mitte der Grundfläche steht, berechnet man als

V = \( \frac{1}{3} \) * Grundfläche * Höhe

In der nun korrigierten Aufgabenstellung ist die Grundfläche ein Dreieck mit dem Flächeninhalt

A = \( \frac{1}{2} \) * 5 m * 6,036 m

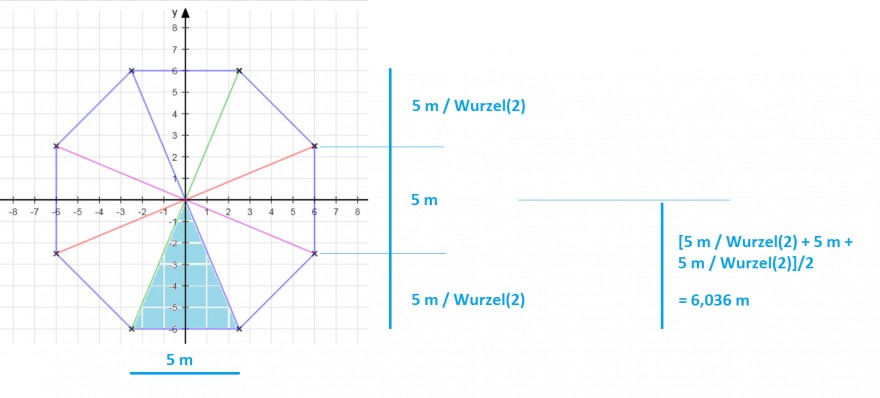
Die Diagonale eines Quadrats ist immer = \( \sqrt{2} \) * Seitenlänge, und entsprechend die Seitenlänge = Diagonale / \( \sqrt{2} \)

Das Volumen der Pyramide ausgerechnet mit der oben angegebenen Formel ist also 20,12 m³ und das Volumen des Dachstocks das Achtfache davon, nämlich 160,96 m³.

---

klasse! Jetzt hab auch ich es verstanden. *freu*

Vielen herzlichen Dank für die ausführliche Beschreibung. So sollte Mathe immer vermittelt werden!

Liebe Grüße

---

Gerne geschehen. Du hast die Existenz von Messfehlern entdeckt: Was auf der Zeichnung gemessen wurde, waren nicht exakt 6 Meter. Bei mir hat die Wortwahl "von der Aussenkante zur Mitte sind genau 6 m" zunächst getriggert, dass es wirklich "genau" 6 Meter seien. Darum war meine erste Lösung falsch. "Exakt" sind nur die 5 Meter Aussenkante. Rechnen ist immer genauer als messen, denn beim Messen gibt es Messfehler. Dass man dich zunächst mit so Sachen wie \( tan \, 22.5° \) und \( \int \) behelligt hatte, ist der Tatsache geschuldet, dass nicht klar war, dass du in der 8. Klasse bist.

Answer 2

Hallo,

im Prinzip ist es eine Pyramide mit einer geleichmäßig achteckigen Grundfläche,

die einzelnen Dreiecke sind gleichschenklig

die höhe im Dreieck ist h = \( \sqrt{6²-2,5²} \)  = 5,45

die Fläche des Dreieckes ist dan A = (5,45 *5) /2  =13,625

die Grundfläche der Pyramide ist 8*A= 109

für das Volumen V = 1/3 G *h nehmen   V = 145.333m³

Comments

Oh je, da steige ich noch nicht ganz durch. Die 145.333m³ ist dann das Volumen des gesamten Dachstocks, ich muss diese Zahl dann also durch 8 teilen, um nur einen Teilabschnitt berechnet zu haben. Richtig ?

Answer 3

Ich habe eine 8 eckige Grundfläche als Dachgeschoss. Die Spitze in der Mitte ist 4m hoch. Jede Aussenkante ist 5m lang. Mittig gemessen von der Aussenkante zur Mitte sin genau 6m.

Ich berechne zuerst 1 Dreieck der Grundfläche
Grundseite 5 m
höhe Dreieck : 6 m
A = 5 * 6 / 2 = 15 m^2

Das Dreick kommt 8 mal vor
A = 15 * 8 = 120 m^2

Das Volumen eines spitz nach oben
zulaufenden Körpers ist
V = 1/ 3 * A * h
h = 4 m
V = 1/3 * 120 * 4 = 160 m^3

Müßte so sein.
Bei Bedarf nachfragen.

Comments

Hallo, vielen herzlichen Dank für die Antwort.

ich bin jetzt ein wenig verwirrt. Ich habe nun 3 Antworten auf meine Frage bekommen, mit drei unterschiedlichen Ergebnissen. Ich als Schüler einer achten Klasse, bin da überfragt, welches nun die richtige Antwort ist.

Antwort 1: 145.333m³

Antwort 2: 159 m³

Antwort 3: 160m³

Zumindest liegen 2 und 3 nahe beieinander.

Was mache ich jetzt am besten ?

---

Ich habe die Angaben zu c = 5 m und
h(c) = 6 m aus der Aufgabenstellung
übernommen.
Ein anderer Kommentator hat darauf
aufmerksam gemacht das dies nicht
so ganz stimmen kann.

Hast du den Originalfragetext ?

mfg Georg

---

Guten Morgen,

im original Text steht:

Stelle dir ein 8 eckiges Gebäude vor. Die Aussenwände sind jeweils 5m lang. Die Spitze des Daches ist 7m hoch. Das Erdgeschoss ist 3m hoch.

Aufgaben:

a) Zeichne eine Ansicht des Gebäudes von oben. → Habe ich gemacht (siehe Link)

b) Berechne die Grundfläche des Gebäudes. → Habe ich gemacht (Ich habe die Fläche zu einem Quadrat erweitert und die 4 dadurch entstanden Dreiecke in den Ecken wieder abgezogen.

c) Berechne das Volumen des Erdgeschosses → Habe ich gemacht.

d) Berechne das Volumen des Dachgeschosses. Nutze zur einfacheren Berechnung einen Teilabschnitt des Daches und rechne es entsprechend hoch.

Andere Maße sind mir nicht gegeben. Wenn ich es zeichne, passt es auch genau. Warum dann die Maße nicht stimmen können, erschließt sich mir nicht. ???

---

Stelle dir ein 8 eckiges Gebäude vor. Die Aussenwände sind jeweils 5m lang

Der obere Winkel in einem Dreieck ist
360 / 8 = 45 °
Halbiere ich das Dreieck auf 2 rechtwinklige
Dreiecke ist der obere Winkel 22.5 °.

c = 5/2 m
Die Höhe h(c)
tan(22.5) = 2.5 / h(c)
h(c) ist = 6.0355 m also nicht 6 m

Die Fläche eines Teiildreiecks ist
5 * 6.0355 / 2 = 15.0888 m^2
Die Gesamtgrundfläche ist
A = 15.0888 * 8 = 120.71 m^2

h = 7 minus 3 = 4 m
V ( Dachgeschoß ) = 1/3 * A * h
V ( Dachgeschoß ) = 1/3 * 120.71 * 4
V ( Dachgeschoß ) = 160.95 m^3

V ( Erdgeschoß ) = A * 3 = ...