Aufgabe
Bestimmen Sie den Schnittwinkel und die Gleichung der Schnittgeraden der durch die Punkte P1 (1|2|3), P2 (2|3|1), P3 (−3|0|2) und Q1 (3|2|1), Q2 (−1| − 2| − 3), Q3 (0|1|2) definierten beiden Ebenen.
Mein Lösungsweg:
Ich habe nur eine Frage zur Berechnung des Schnittwinkels.
Dazu habe ich zuerst von beiden Ebenden die beiden Richtungsvektoren ausgerechnet und gleich das Vektorprodukt:
P1P2 x P1P3 = (-5 | 9 | 2) → sollte ein Vektor darstellen
Q1Q2 x Q1Q3 = (-8 | 16 | -8) → sollte ein Vektor darstellen
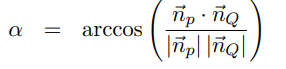
Text erkannt:
\( \alpha=\arccos \left(\frac{\vec{n}_{p} \cdot \vec{n}_{Q}}{\left|\vec{n}_{p}\right|\left|\vec{n}_{Q}\right|}\right) \)
Dann bekomme ich für alpha = 35.17° bekommen. Dies ist mir auch alles klar. Meine Frage ist jetzt: Müsste ich dies nicht noch so ausrechnen 90° - 35.17° = 54.83°. Ich berechne ja den Schnittwinkel der beiden Normalenvektoren.
Vielen Dank im Voraus!