Setze beide Gleichungen gleich:
\(3 x^{2}-x+3y^{2}-z+2=3x^{2}-x+y^{2}-2y-z+6\) ⇔
\(3y^{2}+2=y^{2}-2y+6\) ⇔
\( y^{2}+y-2=0\) ⇔
\( y_{1}=1\) und \(y_{2}=-2\)
Einsetzen von \( y_{1}=1\) in eine der beiden Ausgangsgleichungen ergibt (ich nehme hier die erste):
\(3x^{2}-x+3+2=z\) ⇔
\(z =3x^{2}-x+ 5\)
Einsetzen von \( y_{2} =-2\) in eine der beiden Ausgangsgleichungen ergibt (ich nehme wieder die erste):
\(3x^{2}-x+12+2=z\) ⇔
\(z=3x^{2}-x+ 14\)
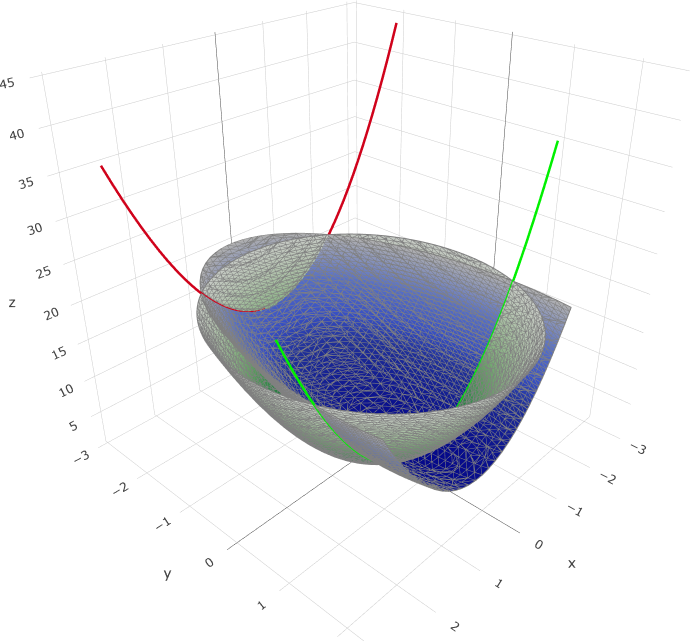
Parametrisieren:
\( \vec{r_{1}} (t)=\begin{pmatrix} t\\1\\3t^2-t+5 \end{pmatrix} \), \( \vec{r_{2}} (t)=\begin{pmatrix} t\\-2\\3t^2-t+14 \end{pmatrix} \), \(t ∈ [-∞,+∞]\)