Aufgabe:
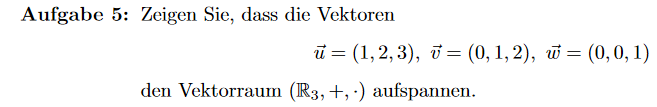
Text erkannt:
Aufgabe 5: Zeigen Sie, dass die Vektoren
$$ \vec{u}=(1,2,3), \vec{v}=(0,1,2), \vec{w}=(0,0,1) $$
den Vektorraum \( \left(\mathbb{R}_{3},+, \cdot\right) \) aufspannen.
… Lösung:
Text erkannt:
Aufgabe 5: Es ist zu zeigen, dass ein beliebiger Vektor \( (a, b, c) \in \mathbb{R}_{3} \) eine Linearkombination von \( \vec{u}, \vec{v}, \vec{w} \) ist, d.h. es muss gelten für \( x, y, z \in \mathbb{R} \) :
$$ (a, b, c)=x \cdot \vec{u}+y \cdot \vec{v}+z \cdot \vec{w} $$
Hieraus ergibt sich das LGS
$$ \begin{array}{r} x=a \\ 2 x+y=b \\ 3 x+2 y+z=c \end{array} $$
und durch rekursives Berechnen \( x=a, y=b-2 a, z=c-2 b+a \in \mathbb{R} \), was \( \mathrm{zu} \) zeigen war.
Text erkannt:
Aufgabe 5: Es ist zu zeigen, dass ein beliebiger Vektor \( (a, b, c) \in \mathbb{R}_{3} \) eine Linearkombination von \( \vec{u}, \vec{v}, \vec{w} \) ist, d.h. es muss gelten für \( x, y, z \in \mathbb{R} \) :
$$ (a, b, c)=x \cdot \vec{u}+y \cdot \vec{v}+z \cdot \vec{w} $$
Hieraus ergibt sich das LGS
$$ \begin{aligned} x &=a \\ 2 x+y &=b \\ 3 x+2 y+z &=c \end{aligned} $$
und durch rekursives Berechnen \( x=a, y=b-2 a, z=c-2 b+a \in \mathbb{R} \), was \( \mathrm{zu} \) zeigen war.
Ich verstehe den Ansatz, da die 3 Vektoren ja den gesamten Vektorraum aufspannen, muss jeder Veektor durch
Linearkombination der Vektoren u,v,w gebildet werden können,
jedoch verstehe ich diesen Teil nicht ganz

Text erkannt:
Aufgabe 5: Es ist zu zeigen, dass ein beliebiger Vektor \( (a, b, c) \in \mathbb{R}_{3} \) eine Linearkombination von \( \vec{u}, \vec{v}, \vec{w} \) ist, d.h. es muss gelten für \( x, y, z \in \mathbb{R} \) :
$$ \begin{array}{l} \qquad(a, b, c)=x \cdot \vec{u}+y \cdot \vec{v}+z \cdot \vec{w} \\ \text { Hieraus ergibt sich das LGS } \\ \qquad \begin{aligned} x &=a \\ 2 x+y &=b \\ 3 x+2 y+z &=c \end{aligned} \end{array} $$
und durch rekursives Berechnen \( x=a, y=b-2 a, z=c-2 b+a \in \mathbb{R} \), was zu
mwar.
Wie wird dieses Gleichungssystem genau gebildet und was sagt das aus?,
Vielen Dank im Voraus!