Zeigen Sie: Das Betriebsoptimum liegt bei etwa 14,6 \mathrm{ME} .

Question

Text erkannt:

1 Die Gesamtkosten eines Polypolisten in Abhängigkeit von der Ausbringungsmenge \( x \) in Mengeneinheiten (ME) werden beschrieben durch die Funktion \( \mathrm{K} \) mit \( \mathrm{K}(\mathrm{x})=\frac{1}{4} \mathrm{x}^{3}-6 \mathrm{x}^{2}+50 \mathrm{x}+280 ; \mathrm{K}(\mathrm{x}) \) in \( \mathrm{GE} \). Die Kapazitätsgrenze liegt bei \( 24 \mathrm{ME} \).
Die produzierte Ware wird für \( 44 \mathrm{GE} \) pro \( \mathrm{ME} \) verkauft.
a) Zeigen Sie: Das Betriebsoptimum liegt bei etwa \( 14,6 \mathrm{ME} \). Bestimmen Sie die langfristige Preisuntergrenze.
b) Ermitteln Sie die kurzfristige Preisuntergrenze.
2 Die Gesamtkosten für ein Produkt der HOW AG werden bestimmt durch die Funktion \( \mathrm{K} \) mit \( \mathrm{K}(\mathrm{x})=0,01 \mathrm{x}^{3}-6 \mathrm{x}^{2}+1500 \mathrm{x}+100000, \mathrm{x} \in[0 ; 700] \)
a) Ein Verkaufspreis von \( 1500 \mathrm{GE} \) pro \( \mathrm{ME} \) sichert eine verlustfreie Produktion. Nehmen Sie
Stellung zu dieser Behauptung. Nennen Sie eine mögliche Produktionsmenge.
b) Die Geschäftsleitung behauptet, dass der Verkaufspreis für eine verlustfreie Produktion bis auf 910 GE/ME gesenkt werden kann. Überprüfen Sie diese Behauptung. Berechnen Sie die Produktionsmenge, die dann produziert und verkauft wird.

Comments

Willst Du das wissen was Du im Titel geschrieben hast, oder das was in der Aufgabe steht?

Das Betreibsoptimum ist beim Minimum der Stückkosten.

Die Stückkosten sind Gesamtkosten / Anzahl.

---

die ganze aufgabe bitte

Answer 1

1a)

Das Betriebsoptimum ist beim Minimum der Stückkosten.

Die langfristige Preisuntergrenze ist ein Synonym zu Betriebsoptimum.

1b)

Das Betriebsminimum ist beim Minimum der variablen Stückkosten.

Die kurzfristige Preisuntergrenze ist ein Synonym zu Betriebsminimum.

Die variablen Kosten sind die Gesamtkosten minus die Fixkosten.

Die Fixkosten sind K(0).

2a)

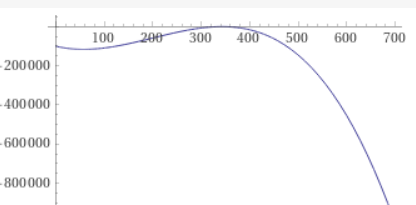
Die Produktion ist "gesichert verlustfrei", wenn der Gewinn im angegebenen Bereich von 0 bis 700 nie negativ ist.

Der Gewinn ist gleich Ertrag minus Gesamtkosten.

Der Ertrag ist gleich Anzahl mal Preis.

Es gibt im möglichen Produktionsbereich Verlust- und Gewinnzonen.

Die Gewinnzone findest Du zwischen den Nullstellen der Gewinnfunktion.

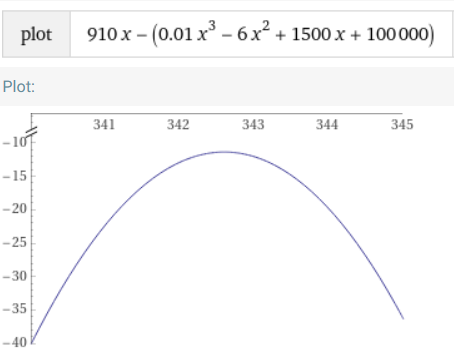
2b)

Bei einem Preis von 910 gibt es keine Gewinnzone: