Grenzwert mit L'Hospital von x * ln((2x+3)/(2x-1))

Question

Aufgabe:

Grenzwert von \( \lim\limits_{x\to\infty}(x * ln(\frac{2x+3}{2x-1})) \) berechnen

Problem/Ansatz:

Ich schaffe es immer nur bis hier und rechne mich dann um Kopf und Kragen. Es wäre super, wenn ich Tipps zur richtigen Lösung bekommen könnte.

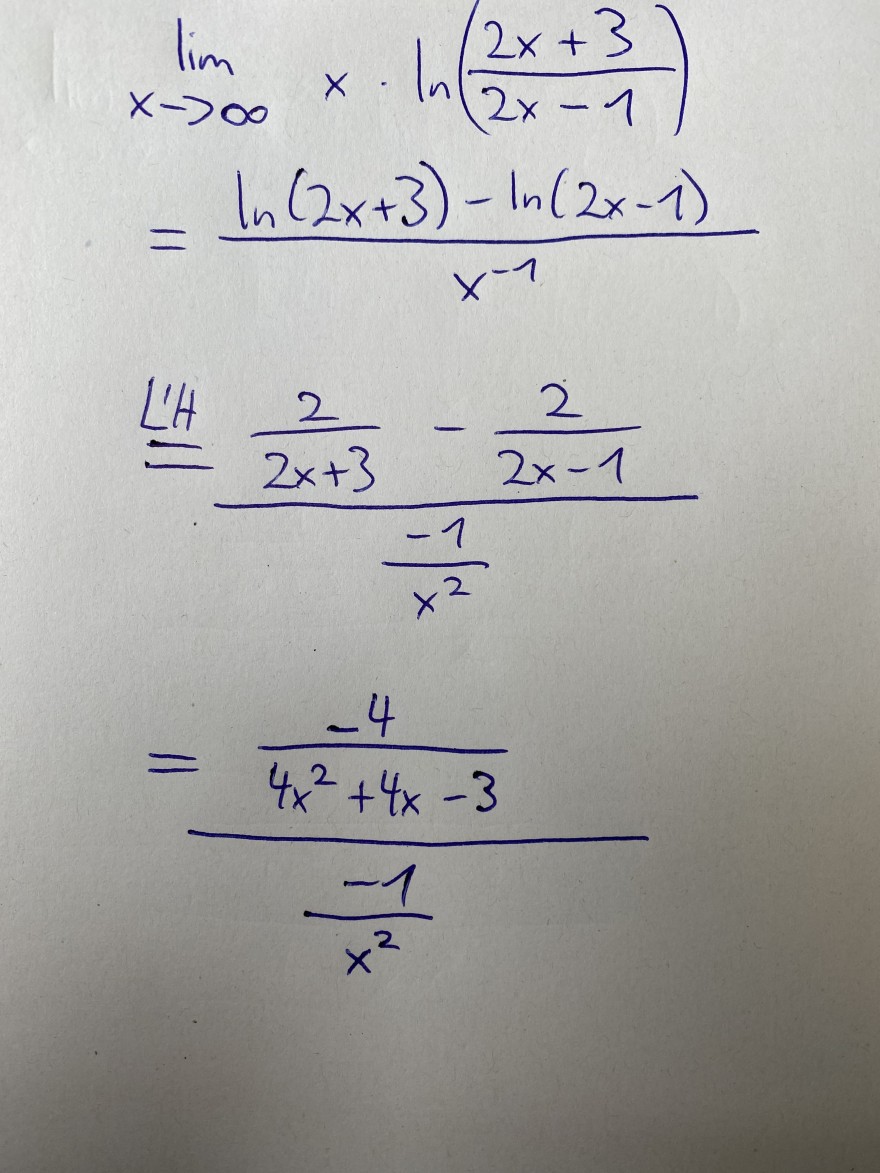
Text erkannt:

\( \lim \limits_{x \rightarrow \infty} x \cdot \ln \left(\frac{2 x+3}{2 x-1}\right) \)
\( =\frac{\ln (2 x+3)-\ln (2 x-1)}{x^{-1}} \)
\( \frac{L^{\prime} H}{=\frac{2}{2 x+3}-\frac{2}{2 x-1}}{\frac{-1}{x^{2}}} \)
\( \frac{=\frac{-4}{4 x^{2}+4 x-3}}{\frac{-1}{x^{2}}} \)

Answer 1

Vermutlich hast du bei deiner letzten Umformung den Faktor 2 vergessen.
Statt -4 muss es -8 heißen:$$\ldots=\lim_{x\to\infty}\frac{\frac{-8}{4x^2+4x-3}}{\frac{-1}{x^2}}=\lim_{x\to\infty}\frac{8x^2}{4x^2+4x-3}=\lim_{x\to\infty}\frac8{4+\frac4x-\frac3{x^2}}=\frac8{4+0-0}=2.$$