Hallo Silvia, vielen Dank für den Link zum matheretter. Dieser schlägt den Bogen von
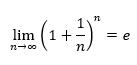
Text erkannt:
\( \lim \limits_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n}=e \)
zu
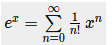
Text erkannt:
\( e^{x}=\sum \limits_{n=0}^{\infty} \frac{1}{n !} x^{n} \)
statt in die umgekehrte Richtung. Auch nicht schlecht! Jetzt wäre zum Abschluss noch der mathematisch korrekte Beweis interessant, wie man von der Eulerschen Zahl e

Text erkannt:
\( \begin{aligned} e &=1+\frac{1}{1}+\frac{1}{1 \cdot 2}+\frac{1}{1 \cdot 2 \cdot 3}+\frac{1}{1 \cdot 2 \cdot 3 \cdot 4}+\cdots \\ &=\frac{1}{0 !}+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}+\frac{1}{4 !}+\cdots \\ &=\sum \limits_{k=0}^{\infty} \frac{1}{k !} \end{aligned} \)
auf die Formel
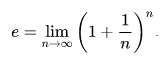
Text erkannt:
\( e=\lim \limits_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n} \)
kommt. Aber eigentlich bin ich schon zufrieden.