Inverse einer Matrix bestimmen

Question

Aufgabe:

Sei K ein Körper und seien a,b,c,d,e,f ∈ K sowie A:= (Matrix im Bild) ∈ M₃(K).
Wir sollen folgende Umkehrung angeben: Wenn a,d,f ∈ K {0} gilt, so ist A invertierbar in (M₃(K),., I₃) und es lässt sich eine Inverse explizit angeben.

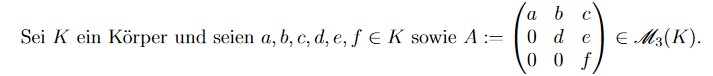
Problem:

Ich steh hier irgendwie etwas aufm Schlauch, wie ich aus der gegebenen Matrix das Inverse herausrechne müsste.

Vielen Dank für jegliche Hilfe.

Text erkannt:

Sei \( K \) ein Körper und seien \( a, b, c, d, e, f \in K \) sowie \( A:=\left(\begin{array}{ccc}a & b & c \\ 0 & d & e \\ 0 & 0 & f\end{array}\right) \in \mathscr{M}_{3}(K) \).

Answer 1

Forme

        \(\begin{pmatrix}a & b & c &1&0&0\\ 0 & d & e &0&1&0\\ 0 & 0 & f&0&0&1\end{pmatrix}\)

mit elementaren Zeilenumformungen so um, dass in den ersten drei Spalten die Einheitsmatrix steht. In den Spalten 4 bis 6 steht dann die inverse Matrix von \(A\).