Hallo,
(die Frage riecht nach Lehramtstudium - oder?)
Der 2.Strahlensatz besagt, wenn zwei durch einen Punkt \(Z\) verlaufende Geraden durch zwei Parallelen, die \(Z\) nicht enthalten, geschnitten werden, dann verhalten sich die Abschnitte auf den Parallelen wie die ihnen entsprechenden, vom Punkt \(Z\) aus gemessenen Strecken auf jeweils derselben Geraden.
Die Umkehrung könnte heißen:
wenn zwei durch einen Punkt \(Z\) verlaufende Geraden durch zwei weitere Geraden \(g^*\) und \(h\), die \(Z\) nicht enthalten, geschnitten werden, und die Abschnitte auf \(g^*\) und \(h\) verhalten sich genauso wie die vom Punkt \(Z\) aus gemessenen Strecken auf jeweils derselben Geraden, dann verlaufen \(g^*\) und \(h\) parallel.
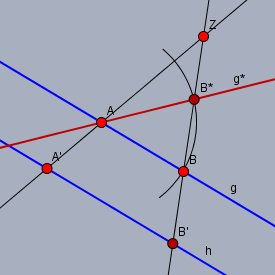
Im Bild sind die beiden Parallele (blau), und es gilt (2. Strahlensatz)$$(g=(AB)) \parallel (h=(A'B')) \implies \frac{|AB|}{|A'B'|} = \frac{|AZ|}{|A'Z|}$$Es lässt sich i.A. aber ein Punkt \(B^*\) finden, mit \(|AB|=|AB^*|\), für den genauso gilt$$\frac{|AB^*|}{|A'B'|} = \frac{|AZ|}{|A'Z|}$$es gilt aber nicht zwingend, dass dann \((g^*=(AB^*)) \parallel (h=(A'B'))\) ist. Wie in der Skizze oben zu sehen ist.