Der 2. Strahlensatz lautet:
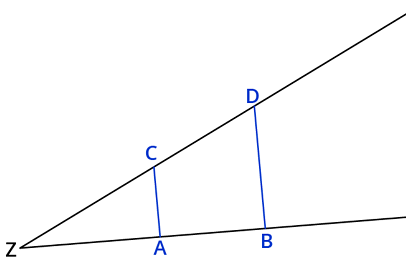
Sind \(\overline{AC}\) und \(\overline{BD}\) parallel, so sind die Verhältnisse \(\overline{AC}:\overline{ZA}\) und \(\overline{BD}:\overline{ZB}\) gleich.
Die Umkehrung lautet: Sind die Verhältnisse \(\overline{AC}:\overline{ZA}\) und (\overline{BD}:\overline{ZB}\) gleich, so sind (\overline{AC}\) und \(\overline{BD}\) parallel.
Gegenbeispiel: Verschiebe den Punkt \(C\) so auf dem Strahl zu einem Punkt \(C'\), so dass \(\overline{AC}=\overline{AC'}\) gilt. Schlage dazu einen Kreisbogen um \(A\) mit dem Radius \(\overline{AC}\). Der Punkt \(C'\) ist dann der zweite Schnittpunkt des Strahls mit dem Kreisbogen. Dass die Parallelität dann nicht erfüllt ist, ist dann sofort ersichtlich.