Folgende Funktion gilt es zu Differenzieren.
Es sind auch zwei Lösungswege angegeben, jedoch komme ich bei den rot markierten Stellen nicht weiter, kann mir jemand die Stellen erklären?
Text erkannt:
\( f(x)=\frac{4 x}{\sqrt{x+1}}=\frac{4 x}{(x+1)^{\frac{1}{2}}} \)
Lösung:
1. Lösungsweg:
\( \begin{array}{l} f^{\prime}(x)=\left(\frac{4 x}{(x+1)^{\frac{1}{2}}}\right)^{\prime}=\left|\begin{array}{c} \text { Quotienten- } \\ \text { regel } \end{array}\right|=\frac{(4 x)^{\prime}(x+1)^{\frac{1}{2}}-4 x\left((x+1)^{\frac{1}{2}}\right)^{\prime}}{\left((x+1)^{\frac{1}{2}}\right)^{2}}=\frac{4(x+1)^{\frac{1}{2}}-4 x \frac{1}{2}(x+1)^{\frac{1}{2}-1}}{(x+1)^{\frac{2}{2}}}= \\ =\frac{4(x+1)^{\frac{1}{2}}-2 x(x+1)^{-\frac{1}{2}}}{x+1}=\frac{4(x+1)^{\frac{1}{2}}-\frac{2 x}{(x+1)^{\frac{1}{2}}}}{x+1}=\frac{4\left((x+1)^{\frac{1}{2}}\right)^{2}-2 x}{(x+1)^{\frac{1}{2}}}= \\ =\frac{4(x+1)-2 x}{(x+1)(x+1)^{\frac{1}{2}}}=\frac{4 x+4-2 x}{(x+1) \sqrt{x+1}}=\frac{2 x+4}{\underline{\underline{(x+1)^{3}}}}=\frac{2(x+2)}{\sqrt{\sqrt{(x+1)^{3}}}} \\ \end{array} \)
Text erkannt:
\( =\frac{4(x+1)-2 x}{(x+1)(x+1)^{\frac{1}{2}}}=\frac{4 x+4-2 x}{(x+1) \sqrt{x+1}}=\frac{2 x+4}{\underline{\sqrt{(x+1)^{3}}}}=\frac{2(x+2)}{\underline{\underline{\sqrt{(x+1)^{3}}}}} \)
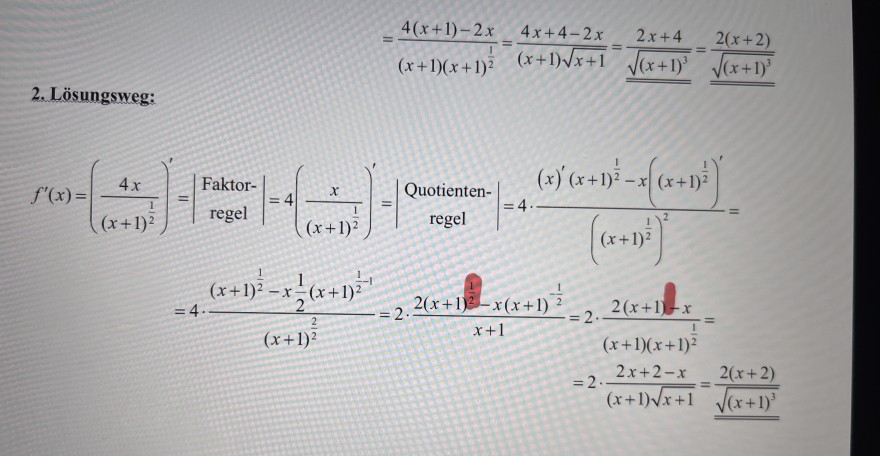
2. Lösungsweg:
\( \begin{array}{l} f^{\prime}(x)=\left(\frac{4 x}{(x+1)^{\frac{1}{2}}}\right)^{\prime}=\left|\begin{array}{c} \text { Faktor- } \\ \text { regel } \end{array}\right|=4\left(\frac{x}{(x+1)^{\frac{1}{2}}}\right)^{\prime}=\left|\begin{array}{c} \text { Quotienten- } \\ \text { regel } \end{array}\right|=4 \cdot \frac{(x)^{\prime}(x+1)^{\frac{1}{2}}-x\left((x+1)^{\frac{1}{2}}\right)^{\prime}}{\left((x+1)^{\frac{1}{2}}\right)^{2}}= \\ =4 \cdot \frac{(x+1)^{\frac{1}{2}}-x \frac{1}{2}(x+1)^{\frac{1}{2}-1}}{(x+1)^{\frac{2}{2}}}=2 \cdot \frac{2(x+1)^{\frac{1}{2}}-x(x+1)^{-\frac{1}{2}}}{x+1}=2 \cdot \frac{2(x+1)-x}{(x+1)(x+1)^{\frac{1}{2}}}= \\ =2 \cdot \frac{2 x+2-x}{(x+1) \sqrt{x+1}}=\frac{2(x+2)}{\underline{\sqrt{(x+1)^{3}}}} \end{array} \)