Aufgabe:

Text erkannt:
Aufgabe 4: Funktionen Für welche Werte des reellen Parameters \( a \) ist die Funktion
\( f(x)=\left\{\begin{array}{ll}\frac{x^{2}+x-2}{x-1} & \text { für } \quad x<1, \\ x+a \quad \text { fiir } \quad 1 \leq x \leq 2, \\ \frac{(x-2)(x+a)}{x^{2}-3 x+2} & \text { für } \quad 2<x\end{array}\right. \)
a) in \( x=1 \) stetig?
b) in \( x=2 \) stetig?
Problem/Ansatz:
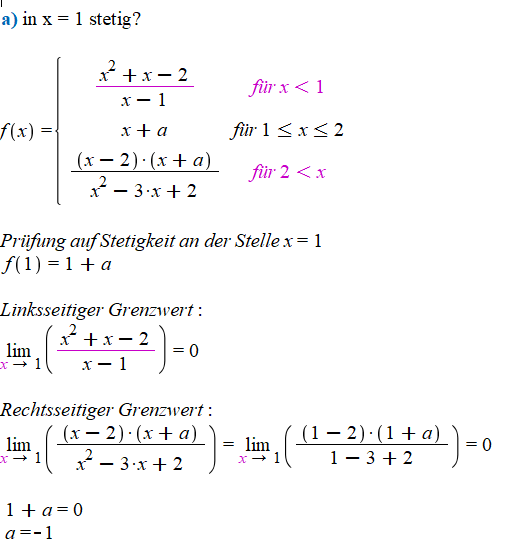
Text erkannt:
a) in \( \mathrm{x}=1 \) stetig?
\( f(x)=\left\{\begin{array}{cc}\frac{x^{2}+x-2}{x-1} & \text { fiir } x<1 \\ x+a & \text { für } 1 \leq x \leq 2 \\ \frac{(x-2) \cdot(x+a)}{x^{2}-3 \cdot x+2} & \text { fiir } 2<x\end{array}\right. \)
Prifung auf Stetigkeit an der Stelle \( x=1 \) \( f(1)=1+a \)
Linksseitiger Grenzwert:
\( \lim \limits_{x \rightarrow 1}\left(\frac{x^{2}+x-2}{x-1}\right)=0 \)
Rechtsseitiger Grenzwert:
\( \lim \limits_{x \rightarrow 1}\left(\frac{(x-2) \cdot(x+a)}{x^{2}-3 \cdot x+2}\right)=\lim \limits_{x \rightarrow 1}\left(\frac{(1-2) \cdot(1+a)}{1-3+2}\right)=0 \)
\( 1+a=0 \)
\( a=-1 \)
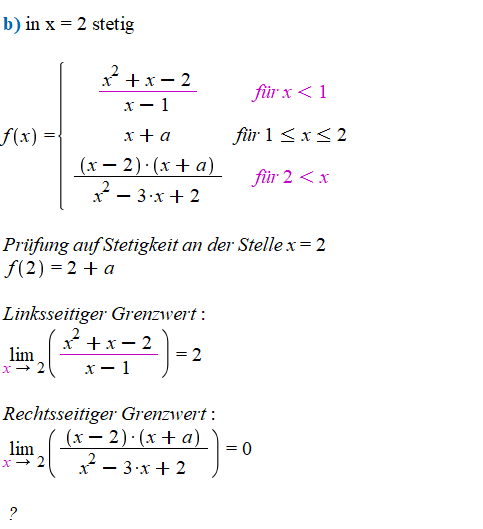
Text erkannt:
b) in \( \mathrm{x}=2 \) stetig
\( f(x)=\left\{\begin{array}{cc}\frac{x^{2}+x-2}{x-1} & \text { fiir } x<1 \\ x+a & \text { fur } 1 \leq x \leq 2 \\ \frac{(x-2) \cdot(x+a)}{x^{2}-3 \cdot x+2} & \text { fiir } 2<x\end{array}\right. \)
Prifung auf Stetigkeit an der Stelle \( x=2 \) \( f(2)=2+a \)
Linksseitiger Grenzwert:
\( \lim \limits_{x \rightarrow 2}\left(\frac{x^{2}+x-2}{x-1}\right)=2 \)
Rechtsseitiger Grenzwert:
\( \lim \limits_{x \rightarrow 2}\left(\frac{(x-2) \cdot(x+a)}{x^{2}-3 \cdot x+2}\right)=0 \)
\( ? \)
Hallo, bei der Aufgabe a) ist die Funktion für x=-1 stetig.
Müsste richtig sein.
Aber bei Aufgabe b) komme ich nicht richtig weiter.
Vielleicht kann mir jemand helfen.
Vielen Dank
Gruß Jan