Hallo Hanny,
Aufgabe 1
a) \(y=-3x+7\)
-3 ist die Steigung, bei 7 schneidet der Graph die y-Achse. Zeichne diesen Punkt ein, gehe eine Einheit nach rechts und dann 3 Einheiten nach unten und zeichne den nächsten Punkt ein. Bei Aufgabe b gehst du vom Schnittpunkt mit der y-Achse eine Einheit nach recht und 0,3 nach oben, bei c) eine nach rechts und 1,2 nach unten und bei d) eine nach rechts und 0,6 nach oben. Alternativ gibst du für x eine beliebige Zahl ein, um einen weiteren Punkt zu erhalten.
zum Beispiel: a) \(y=-3\cdot 2+7=1\), also P (2|1)
Graphisch sieht das so aus:
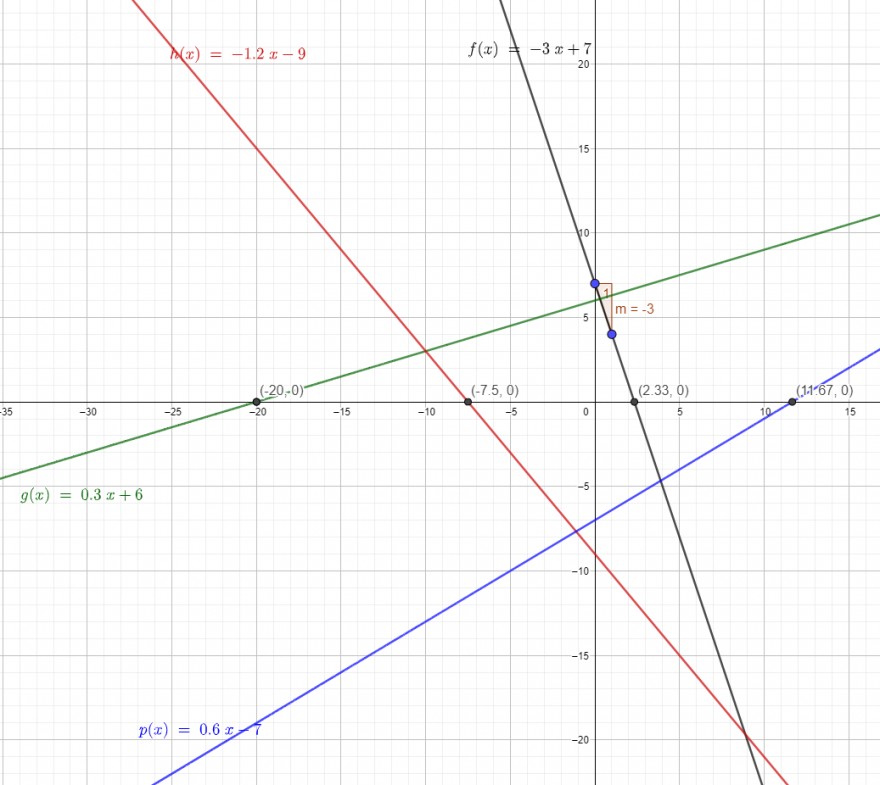
Die Nullstellen berechnest du, indem du die Funktionen = 0 setzt und nach x auflöst:
a)
\(-3x+7=0\\ -3x=-7\\ x=\frac{7}{3}\)
b)
\(0,3x+6=0\\0,3x=-6\\x=-20\)
c)
\(-1,2x-9=0\\-1,2x=9\\ x=-7,5\)
d)
\(0,6x-7=0\\0,6x=7\\ x=\frac{35}{3}\)
Aufgabe 2
Schnittpunkt mit der y-Achse bei 200, Steigung = -1,5
Funktionsgleichung \(y=-1,5x+200\)
b) Nullstelle bestimmen:
\(-1,5x+200=0\\ -1,5x=200 x=\frac{400}{3}\approx133,3\)
c) Setze die Funktionsgleichung = 10 und löse nach x auf:
\(-1,5x+200=10\\ -1,5x=-190\\ x\approx 126,7\)
d) Setze als Steigung -2 ein und berechne die Nullstelle:
\(-2x+200=0\\ -2x=-200\\x=100\)
Also landet der Ballon ca. 33 Sekunden früher.
Gruß, Silvia