Flächeninhalt einer quadratischen Funktion berechnen

Question

Aufgabe:

Der Graph der Funktion f schließt mit der x-Achse eine Fläche vollständig ein. Berechne den
Inhalt dieser Fläche. Durch den Hochpunkt des Graphen der Funktion f verläuft eine Gerade,
die diese Fläche halbiert. Berechne die Schnittstellen dieser Gerade mit der x-Achse.

f(x) = 1/3x³ − 4x² + 12x₋  ∈ ℝ

Problem/Ansatz:

Meine Nullstellen sind x1= 0 und x2=6

ich habe angefangen ein Integral aufzustellen von 0 bis 6. Jedoch weiß ich nicht wie ich weiter vorgehen muss.

kann mir bitte jemand helfen!!!

Answer 1

f(x) = 1/3x^3 − 4x^2 + 12x
Stammfunktion
s ( x ) = 1/12 * x^4  - 4/3* x^3 + 6x^2
[  1/12 * x^4  - 4/3* x^3 + 6x^2 ] zwischen 0 und 6

1/12 * 6^4  - 4/3* 6^3 + 6*6^2  minus
1/12 * 0^4  - 4/3* 0^3 + 6*0^2

36

b.)
du brauchst nur die x-Stelle des Hochpunkts
zu berechnen.

Comments

b.)
siehe Antwort Monty

Answer 2

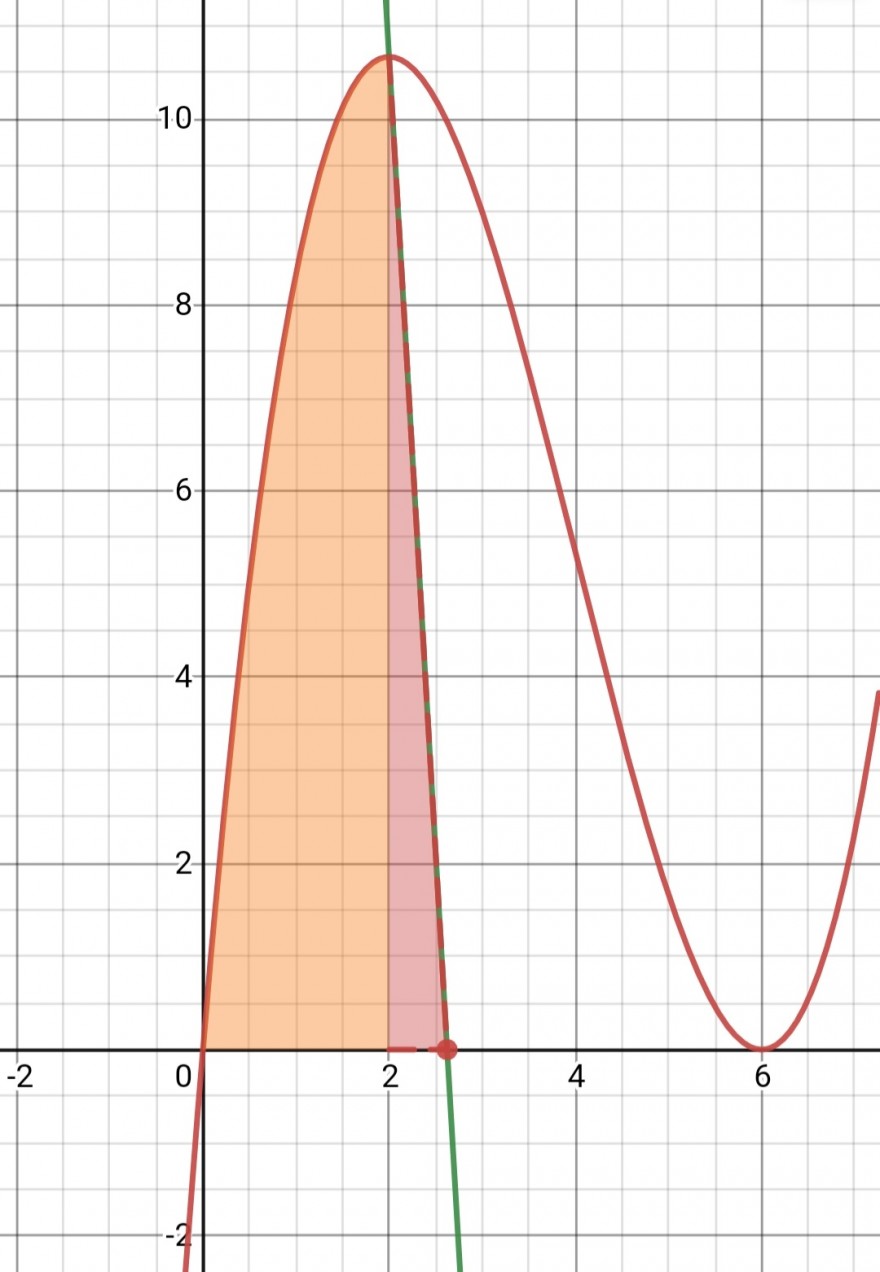
Das Integral von 0 bis 6 ergibt 36.

Davon die Hälfte ist 18.

Der Hochpunkt liegt bei H(2|10,6667) bzw.

H(2 | 32/3).

Das Integral von 0 bis 2 beträgt 14,6667.

Die Gerade durch den Hochpunkt muss also eine Fläche zwischen x=2 und x=c mit der x-Achse einschließen, die den Inhalt

18-14,6667=3,333=10/3

hat. Diese Fläche hat die Form eines rechtwinkligen Dreiecks.

A=0,5*(c-2)*f(2)

10/3=0,5*(c-2)*32/3

10=16*(c-2)

c=2,625

Das ist die Nullstelle der gesuchten Geraden.

Comments

Hallo,

ich habe noch ein Bild hinzugefügt.

:-)