Funktionsterm einer Funktion dritten Grades aufstellen bei einer Auffahrt (Länge 12m, Höhenunterschied 2m)

Question

Aufgabe:

Es gibt eine Auffahrt, die zu einem 2m höher gelegenen Parkplatz führt. Auf einer Strecke von 12m Länge muss ein Höhenunterschied von 2m überwunden werden. Oben und unten soll die Auffahrt ohne Knick waagerecht in die Straße bzw. den Parkplatz übergehen.

Problem/Ansatz:

a) Zeigen Sie, dass sich diese Bedingungen mit Hilfe einer Funktion f dritten Grades verwirklichen lassen, geben Sie einen geeigneten Funktionsterm an.

b) Prüfen Sie, ob die Bedingung einzuhalten ist, dass die maximale Steigung der Auffahrt 20% nicht überschreiten darf.

Ich weiß leider nicht, wie genau ich mit dieser Aufgabe überhaupt anfange... Dass es sich um eine Funktion dritten Grades handeln muss macht für mich Sinn aber wie genau erstelle ich jetzt den Funktionsterm und überprüfe b)? Ich hoffe ihr könnt mir bei meinen Startschwierigkeiten helfen! Im Voraus schonmal vielen Dank an alle <3

Answer 1

Lege das Koordinatensystem so, wie dargestellt. Dann lautet der Ansatz: f(x)=ax³+bx²+cx und

daher f '(x)=3ax²+2bx+c.

f '(0)=0 ergibt : c=0

f '(12)=0 ergibt: 432a+24b=0

P(12|2) ergibt: 2=1728a+144b

Dann ist a= - $\frac{1}{432}$ und b=$\frac{1}{24}$. Beides in den Ansatz einsetzen.

Comments

Ah ja perfekt genau das habe ich gebraucht aber wie genau hast du a und b im Endeffekt ausgerechnet?

---

(1) 432a+24b=0

(2) 2=1728a+144b

ist ein System von zwei Gleichungen mit zwei Unbekannten. Das kannst du doch sicher lösen?

---

Ja, ich komme nur auf versetze Vorzeichen und finde meinen Fehler nicht weshab ich irritiert bin...

I.) 2 = 1728a + 144b

II.) 0 = 432a + 24b             I x4

III.) 4 = 1728a + 96b

I. - III. = IV.

IV.) -2 = 48b                      I : 48

-1/24 = b

b in II.)

0 = 432a + 24 (-1/24)

0 = 432a - 1                      I +1

1 = 432a                           I :432

1/432 = a

---

Der Fehler ist hier:

II.) 0 = 432a + 24b           I x4

III.) 4 = 1728a + 96b

Richtig:

0 = 1728a + 96b

Damit ist I - III

2 = 48b

---

Ah mist was ein blöder Flüchtigkeitsfehler vielen Dank!

Noch eine Frage: bei b) muss ich einfach die zweite Ableitung=0 setzen und das Ergebnis in die erste Ableitung einsetzen oder? Und wenn eine Zahl größer als 0,2 herauskommt ist die Bedingung nicht zu erfüllen...?

---

Genau so ist es.

Answer 2

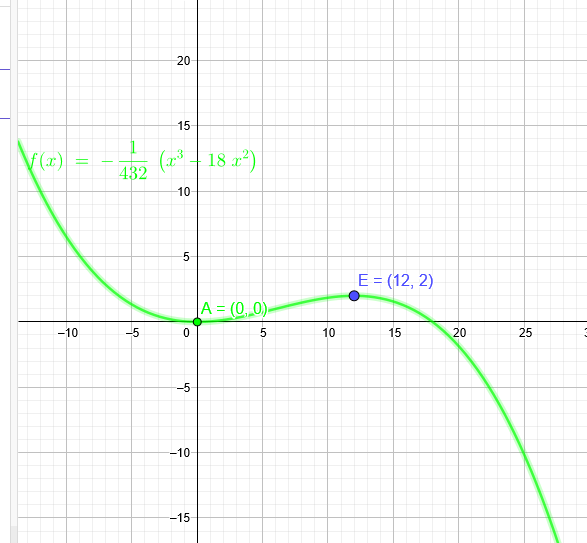
Bei Punkt A(0|0) und bei E(12|2) müssen waagerechte Tangenten vorliegen:

Nullstellenform der Parabel 3.Grades:

f(x)=a*(x-N_1)*(x-N_2)*(x-N_3)

Nun existiert bei A eine doppelte Nullstelle (wegen Minimum an der Stelle):

f(x)=a*x²*(x-N_3)=a*[x³-x²*N_3)

E(12|2)

f(x)=a*[12³-12²*N_3)=a*[1728-144*N_3]

1.) a*[1728-144*N_3]=2 → a= $\frac{2}{1728-144*N_3}$

Nun ist ein Maximum bei E :

f´(x)=a*[3x²-2x*N_3]

f´(12)=a*[3*144-24*N_3]

a*[3*144-24*N_3]=0|:a

3*144-24*N_3=0

N_3=18   ∈  1.)    a= $\frac{2}{1728-144*18}$

a=- $\frac{1}{432}$

f(x)=- $\frac{1}{432}$*(x^3-18x^2)