Fitten einer Funktion an eine Kurve mit Bedingungen (Wellenform)

Question

Aufgabe:

Fläche unterhalb der Kurve [0;10] berechnen. Dazu ist das Fitten einer Funktion an diese Kurve nötig.

Problem/Ansatz:

Leider passt mein Ergebnis einer Funktion nicht 100%ig zu dem Graphen, bzw. ich kriege das Gleichungssystem nicht gelöst. Sowohl mit 4 Bedingungen als auch mit 5. Was mache ich falsch? Kann man die Kurve überhaupt mit einer Funktion 3. Grades fitten?

Ableitungen der Standardfunktion 3. Grades:

Text erkannt:

5 Bedingungen:
1. $\quad f(0)=a^{*}(0)^{3}+b^{*}(0)^{2}+c^{*}(0)+d=2,9$
2. $\quad f(10)=a^{*}(10)^{3}+b^{*}(10)^{2}+c^{*}(10)+d=2,9$
3. $\quad f^{\prime}(2,6)=3 a^{*}(2,6)^{2}+2 b^{*}(2,6)+c=0$
4. $\quad f^{\prime}(7,6)=3 a^{*}(7,6)^{2}+2 b^{*}(7,6)+c=0$
5. $\quad f^{\prime \prime}(5,1)=6 a^{*}(5,1)+2 b=0$
Gleichungssystem mit 5 Bedingungen:
1. $\mathrm{d}=2,9$
2. $\quad f(10)=1000 a+100 b+10 c+d=2,9$
3. $20,28 a+5,2 b+c=0$
4. $173,28 a+15,2 b+c=0$
5. $\quad 30,6 \mathrm{a}+2 \mathrm{~b}=0$

Ich hatte raus, dass a,b und c in dem Fall 0 sind. Das kann ja irgendwie nicht sein...

Wie bekomme ich eine Funktion die dem Graphen möglichst ähnlich sieht?

Wie man die Fläche dann per Integral berechnet weiß ich ;-)

Answer 1

Definiere

> 100%ig zu dem Graphen<

Bild in GeoGebra eingefügt und skaliert auf KO

Optisch würde man sich ggf. mit einem Bezier-Spline (grün, Parameterkurve) am besten rantasten können

oder auch die Stützpunkte eines Polynoms so hin ruckeln, dass man eine in etwa Übereinstimmung hin bekommt Polynom(4) blau ()

$f_1(x):=Fit(\{E,D,G,C,F\}, \{x^4,x^3,x^2,x,1\})$

$\small BL:= \left\{ \left(\frac{1}{5}, \frac{14}{5} \right), \left(\frac{11756231}{2555181}, \frac{1360081}{1227084} \right), \left(\frac{6004885}{983618}, \frac{6455563}{1342836} \right), \left(\frac{48}{5}, 3 \right) \right\}$ - die beiden mittleren Punkte sind die Control-Points zur Anpassung

$\small Q(t):=Sum( \left\{ \left(-t + 1 \right)^{3}, 3 \; t \; \left(-t + 1 \right)^{2}, 3 \; t^{2} \; \left(-t + 1 \right), t^{3} \right\} * (BL ))$

Ich ergänze meine Flächenberechnungen:

Integral( y(Q(t)) Derivative( x(Q(t)),t), -0.015,1.0373) ~ 28.94896295706

Integral(f_1, 0, 10) = 28.97982049784

Comments

Super. Damit komme ich zu einem Ergebnis, das sehr exakt ist. Gibt es auch eine Möglichkeit das näherungsweise oder auch exakt per Hand zu bestimmen. Ich kann schlecht auf Geogebra als Rechenweg verweisen.

---

Hm,

warum nicht?

Wenn Du einfach irgendwelche Stützpunkte festlegst und diese exakt treffen willst, dann schwingt ein Polynom zwischen den Stützpunkten mit wachsendem Grad immer stärker - m.a.W. du hast keine Kontrolle, was zwischen den Stützpunkten abgeht

https://www.geogebra.org/m/Qaed4y4Y

das passt dann ehr nicht mit dem Graph zusammen. Weil je mehr Punkte desto schwingt.

Was ich mit GGB gemacht habe ist eine Polynomregression (ggb command Fit())

https://www.geogebra.org/m/qsE5aQEp

Um Deinen Graph zu treffen muß ich jetzt die Punkte live zurechtrücken und damit das Polynom möglichst exakt auf den Graphen legen. Das kann schwierig werden, weil jede Stützpunkt-Änderung das gesammten Graphen bewegt.

Ähnlich geht es mit den Splines

https://www.geogebra.org/m/urfejea4

der Bezier-Spline (Grad 3 oder 4 in der App) trifft den ersten und letzten Punkt und mit den mittleren beiden Controls (Grad 3), drei (Grad 4) kann man den Verlauf der Kurve anpassen.

===>

Du hast in jedem Verfahren, das Problem die Stützpunkte zu finden, die ein möglichst "exaktes" Ergebnis abliefern. Das läßt sich durch draufschauen nicht ermitteln - das muss man ausprobieren!

Solange niemand hinterfragt, wie die Stützpunkte gewählt wurden bist Du fein raus. Die Rechnung, die Mathematik dahinter, findest Du im CAS der genannten Apps. Für die Rechnung braucht man GGB nicht wirklich - musst Du halt auf was auch immer übertragen...

Rechnerisch am einfachsten ist der Bezier-Spline: Bernstein-Basis-Polynome (Grad 3 genügt) erstellen, Punkte einsetzen - Controls zur Anpassung verwenden - Fertig - Rechnung Q(t) und Integral oben.

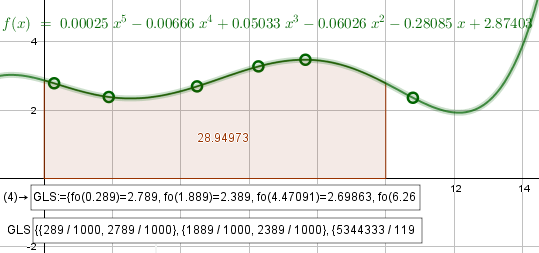
Oder Du nimmst die Punkte

$\small FL \, := \, \left(\begin{array}{rr}0.289&2.789\\1.889&2.389\\4.47091&2.69863\\6.26954&3.2838\\7.64635&3.48049\\10.79335&2.36593\\\end{array}\right)$

und legst mit der ersten App ein Polynom Grad 5 durch - die Rechnung kannst Du dann quasi im CAS abschreiben...

 

Answer 2

Hallo

ich habe Mühe, Werte auf dem computer abzulesen, Kann es sein, dass es eine sin Funktion ist?

falls f(0)=f(10)  ist   ist die Periode 10 die Amplitude (f(7,6)-f(2,6))/2

dann noch Phase und Verschiebung ablesen.

Gruß lul

Comments

Die Idee ist gut. Leider ist das "Tal" tiefer als der "Berg" bei der Wellenform, sodass das leider nicht funktionieren würde meiner Meinung nach. Möglicherweise könnte man dafür 2 Sinusfunktionen verwenden für die beiden Teilstücke rechts und links, aber das wäre natürlich ordentlich Aufwand.

---

Ich meinte "Berg" höher als "Tal" tief :)

---

Hallo

Tal tiefer als Berg, nur wenn du 3 als Mitte nimmst,  wenn es ein sin ist dann geht die Symmetrielinie durch (f(2,6)+f(7,6))/2

Aber inzwischen steht da ja schon eine gute Näherung  mit einem Polynom 3,ten Grades.

lul

---

Der "Schwung" der beiden Bögen stimmt nicht überein. Um die einigermaßen zu treffen muß ich auf ein Polynom Grad 5 gehen - dann stimmt das Ergebnis bis in die zweite Dezimalstelle mit dem des Bezier-Spline zusammen:

Mit kubischen Polynomen kann ich nur einen der Bögen abdecken, auf dem anderen wird immer mehr oder weniger über- oder unterschnitten. Weiß Du was über die Herkunft der Daten ?