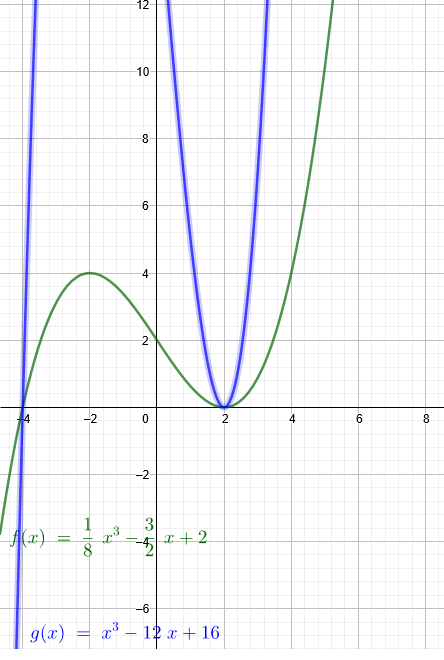
Falls die Funktion so lautet:
f(x) = \( \frac{1}{8} \)x^3 - \( \frac{3}{2} \) x + 2
\( \frac{1}{8} \) x^3 - \( \frac{3}{2} \) x + 2=0|*8
x^3 - 12 x + 16=0
Nun sind eventuell mögliche Nullstellen die positiven wie auch negativen Teiler von 16. Probiere mal mit +-1 und +-2 an.
Hier geht auch folgender Trick: Extremwertbestimmung von:
g(x)=x^3 - 12 x + 16
g´(x)=3x^2-12
3x^2-12=0
x^2=4
x₁=2 → g(2)=2^3 - 12 *2 + 16 =8-24+16=0 Art des Extremum: g´´(x)=6x g´´(2)=6*2 =12> 0 Minimum
x₂ = - 2 (entfällt)
Somit hast du bei x=2 sogar eine doppelte Nullstelle und kannst mit der Polynomdivision die 3. Nullstelle finden:
(x^3 - 12 x + 16):(x-2)^2
(x^3 - 12 x + 16):(x^2-4x+4)=x+4
-(x^3-4x^2+4x)
__________
4x^2-16x+16
-(4x^2-16x+16)
____________________
0