orthogonale Komplement Untervektorraum eines Prähilbertraums

Question

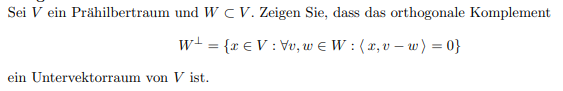
Text erkannt:

Sei \( V \) ein Prähilbertraum und \( W \subset V \). Zeigen Sie, dass das orthogonale Komplement
$$ W^{\perp}=\{x \in V: \forall v, w \in W:\langle x, v-w\rangle=0\} $$
ein Untervektorraum von \( V \) ist.

Problem/Ansatz:

Könnte mir jemand erklären wie ich da vorgehen muss bzw. wie das geht?

Comments

Zeig dass es nicht leer und abgeschlossen bzgl Addition und Skalarmultiplikation ist. Verwende die Bilinearität des Skalarprodukts.