Text erkannt:
Ableitung mit der Quotientenregel:
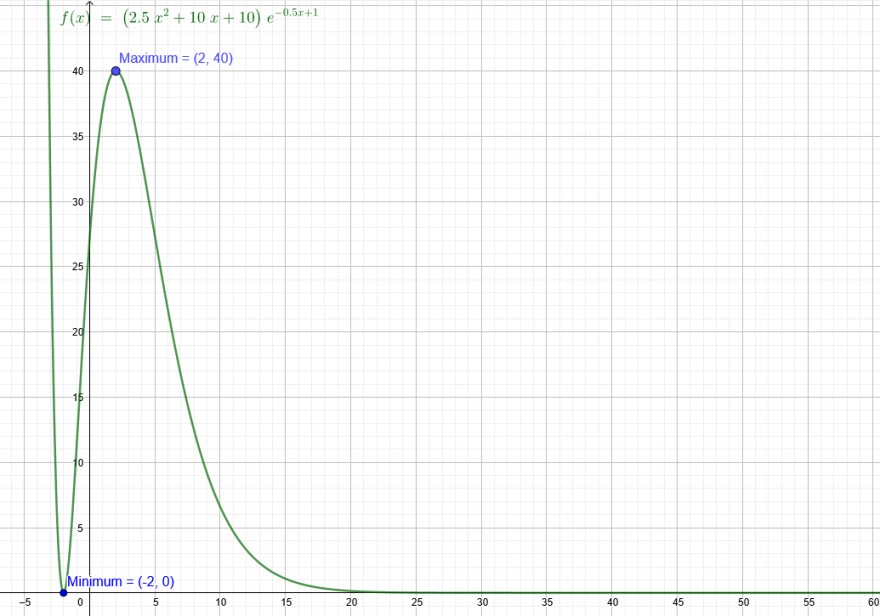
\( A(a)=\left(2,5 a^{2}+10 a+10\right) \cdot e^{-0,5 a+1}=\frac{2,5 a^{2}+10 a+10}{e^{(0,5 a-1)}} \)
A \( \cdot(a)=\frac{(5 a+10) \cdot e^{(0,5 a-1)}-\left(2,5 a^{2}+10 a+10\right) \cdot e^{0,5 a-1} \cdot 0,5}{\left(e^{(0,5 a-1)}\right)^{2}} \)
\( \mathrm{A} \cdot(a)=\frac{(5 a+10)-\left(2,5 a^{2}+10 a+10\right) \cdot 0,5}{e^{(0,5 a-1)}}=\frac{5-1,25 a^{2}}{e^{(0,5 a-1)}} \)
\( A^{\prime} \cdot(a)=\frac{(-2,5 a) \cdot\left(e^{(0,5 a-1)}\right)-\left(5-1,25 a^{2}\right) \cdot\left(e^{(0,5 a-1)}\right) \cdot 0,5}{\left(e^{(0,5 a-1)}\right)^{2}} \)
\( \frac{5-1,25 a^{2}}{e^{(0,5 a-1)}}=0 \)
\( a_{1}=2 \)
\( a_{2}=-2 \)
Art des Extremum:
\( \mathrm{A} \cdot(a)=\frac{-2,5 a-2,5+0,625 a^{2}}{e^{(0,5 a-1)}} \)
A \( \cdots(2)=\frac{-2,5 \cdot 2-2,5+0,625 \cdot 4}{e^{(0,5 \cdot 2-1)}}<0 \rightarrow \) Maximum
\( A \cdot(-2)=\frac{-2,5 \cdot(-2)-2,5+0,625 \cdot 4}{e^{(0,5 \cdot(-2)-1)}}>0 \rightarrow \) Minimum