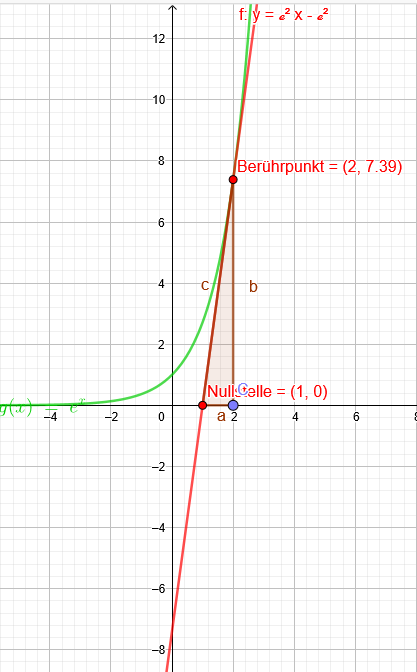
B) Der Graf der natürlichen Exponentialfunktion schließt mit der Tangente im Punkt P(2 | f(2)) und den Koordinatenachsen eine Fläche ein. Berechnen Sie den Inhalt dieser Fläche.
Fläche unter e^x
A_1=\( \int\limits_{0}^{2} \)e^x*dx=e^2-e^0=e^2-1
Nullstelle der Tangente: y=e^2*x-e^2
e^2*x-e^2=0
x=1
Fläche des Dreiecks:
A_2=\( \frac{1}{2} \) *e^2
A=A_1-A_2
A=e^2-1-\( \frac{1}{2} \) *e^2=\( \frac{1}{2} \) *e^2-1