Aufgabe:
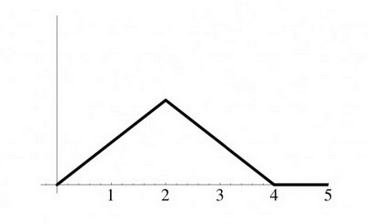
Die Abbildung zeigt den Graphen einer Dichtefunktion \( y=f(x) \) für die Lebensdauer \( x>0 \)
eines elektronischen Gerätes in Jahren.
(a) Bestimmen Sie die Höhe \( h \) des Dreiecks so, dass \( f(x) \) eine Dichtefunktion ist!
(b) Wie groß ist die Wahrscheinlichkeit, dass das Gerät mindestens 3 Jahre lebt (funktioniert)?
(c) Wie groß ist die Wahrscheinlichkeit, dass ein 2 Jahre altes Gerät noch mindestens ein Jahr funktioniert?
(d) Bestimmen Sie den Funktionsterm von \( f ! \)
\( f(x)=\left\{\begin{array}{ll}\text {... für } & 0<x \leq 2 \\ \text {... für } & 2<x \leq 4 \\ \text {... für } & x>4\end{array}\right. \)
(e) Bestimmen Sie Erwartungswert und Varianz der Lebenserwartung \( x \) des Gerätes!
Problem/Ansatz:
Bestimmen Sie die Aufgaben a, b, c, d, e!