Hallo Lilly,
Punktsymmetrie bzgl. eines Punktes \((a|\,b)\) bedeutet$$f(a-u) + f(a+u) = 2b$$Mache Dir das z.B. an Hand folgender Skizze klar
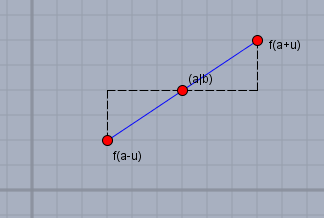
Teile das Integral bei \(a\) in zwei Hälften $$\int\limits_{x=a-R}^{a+R} f(x)\,\text dx = \int\limits_{u=0}^{R}f(a-u)\,\text du + \int\limits_{u=0}^{R}f(a+u)\,\text du$$Gleichzeitig habe ich das \(x\) durch ein \(u\) substituiert. Nun stehen dort zwei Integrale gleicher Länge, die kann ich auch zusammen fassen$$\phantom{=}\int\limits_{x=a-R}^{a+R} f(x)\,\text dx\\= \int\limits_{u=0}^{R}f(a-u)\,\text du + \int\limits_{u=0}^{R}f(a+u)\,\text du\\=\int\limits_{u=0}^{R}f(a-u)+f(a+u)\,\text du\\ = \int\limits_{u=0}^{R} 2b\,\text du \\ = \left.2bu\right|_{u=0}^{R} = 2bR$$Und \(f(a)=b\). Wenn dem nicht so wäre, dann wäre \(f\) auch nicht punktsymmetrisch zu \((a|\,b)\). Das folgt auch aus der ersten Gleichung ganz oben, wenn Du dort \(u=0\) einsetzt.
Gruß Werner