Lineare Regression berechnen.

Question

Für fünf ausgewählte private Haushalte wurden jeweils Monatsdurchschnitte für die Höhe des Nettoeinkommens X (in 1000Euro) und die Höhe der Telefonrechnung Y (in 100 Euro) ermittelt.


Haushalte       x                 y

1                    2.6              2.5

2                    2.1              1.7

3                    1.4              2.0

4                    3.5              3.0

5                  1.7                2.2

a) Berechnen Sie die Koeffizienten der linearen Einfachregression von Y auf X.

Die Koeffizienten der linearen Einfachregression (Y=a+ X*b) lauten:

a =

b=


b) Prognostizieren Sie unter Verwendung der Ergebnisse von Aufgabe a) die Höhe der Telefonrechnung für einen Haushalt mit einem durchschnittlichen Nettoeinkommen von 2300 Euro im Monat. Die Höhe der Telefonrechnung (in Euro) ist:


c) Um wie viel veränderten sich die durchschnittlichen Ausgaben für das Telefon pro Haushalt, wenn das monatliche Nettoeinkommen um 500 Euro steigt ?Die durchschnittlichen Ausgaben stiegen um den Betrag von ..?


d) Berechnen Sie das Bestimmtheitsmaß.

Answer 1

Du könntest zur Kontrolle deiner eigenen Ideen Geogebra benutzen.

Answer 2

Programme um die Koeffizieten ruck-zuck zu
berechnen gibt es jede Menge.
Sollst du die Aufgabe zu Fuß berechnen ?

Comments

Döschwos Paradoxon:

Wer zu Fuß rechnet, benutzt den Kopf mehr.

Answer 3

Man minimiert die Quadrate der Abweichungen zwischen Funktionswert y = a + bx und gemessenem y, um die Koeffizienten a und b zu erhalten.

Das führt zur Regressionsgleichung \( y =  \frac{3187}{2732}+ \frac{673}{1366}x \)

Comments

Die Zielfunktion:

\( \left(\frac{25}{10}-\left(a+\frac{26}{10} b\right)\right)^{2}+\left(\frac{17}{10}-\left(a+\frac{21}{10} b\right)\right)^{2}+\left(2-\left(a+\frac{14}{10} b\right)\right)^{2}+\left(3-\left(a+\frac{35}{10} b\right)\right)^{2}+\left(\frac{22}{10}-\left(a+\frac{17}{10} b\right)\right)^{2} \)

\(= 5 a^{2}-\frac{114}{5} a+\frac{113}{5} a b+\frac{2827}{100} b^{2}-\frac{2711}{50} b+\frac{1349}{50} \)

Das Minimum:

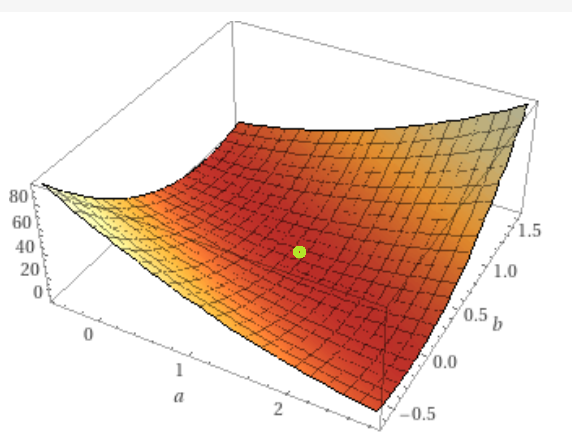
Das Bestimmtheitsmaß:

Dividiere die Summe der quadrierten Abweichungen vom Funktionswert zum Mittelwert von y ("erklärte Quadratsumme", auch SQE sum of squares explained) durch die Summe der quadrierten Abweichungen vom Messwert zum Mittelwert von y ("totale Quadratsumme", auch SST sum of squares total).