Zeigen Sie dass F(x)= -10*(x+1)*e-x eine Stammfunktion von f ist.

Question

Aufgabe:

Zeigen Sie dass F(x)= -10*(x+1)*e^-x  eine Stammfunktion von f ist.

f= f(x)= 10*x*e^-x

Problem/Ansatz:

Mir macht die Ableitung der Stammfunktion Probleme. Kann mir da jemand vielleicht helfen?

LG

Answer 1

Aloha :)

$$F'(x)=\left(-10\cdot(x+1)\cdot e^{-x}\right)'=-10\cdot\left(\underbrace{(x+1)}_{=u}\cdot\underbrace{e^{-x}}_{=v}\right)'$$$$\phantom{F'(x)}=-10\cdot\left(\underbrace{1}_{=u'}\cdot\underbrace{e^{-x}}_{=v}+\underbrace{(x+1)}_{=u}\cdot\underbrace{\overbrace{e^{-x}}^{=\text{äußere Abl.}}\cdot\overbrace{(-1)}^{=\text{innere Abl.}}}_{=v'}\right)$$$$\phantom{F'(x)}=-10\left(e^{-x}-(x+1)e^{-x}\right)=-10(e^{-x}-xe^{-x}-e^{-x})=10x\cdot e^{-x}$$$$\phantom{F'(x)}=f(x)\quad\checkmark$$

Answer 2

Ableitung mit der Quotientenregel:

F(x)= -10*(x+1)*\( e^{-x} \)=\( \frac{-10x-10}{e^{x}} \)

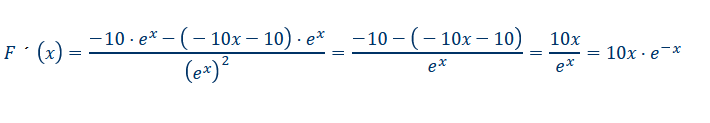
Text erkannt:

\( F \cdot(x)=\frac{-10 \cdot e^{x}-(-10 x-10) \cdot e^{x}}{\left(e^{x}\right)^{2}}=\frac{-10-(-10 x-10)}{e^{x}}=\frac{10 x}{e^{x}}=10 x \cdot e^{-x} \)