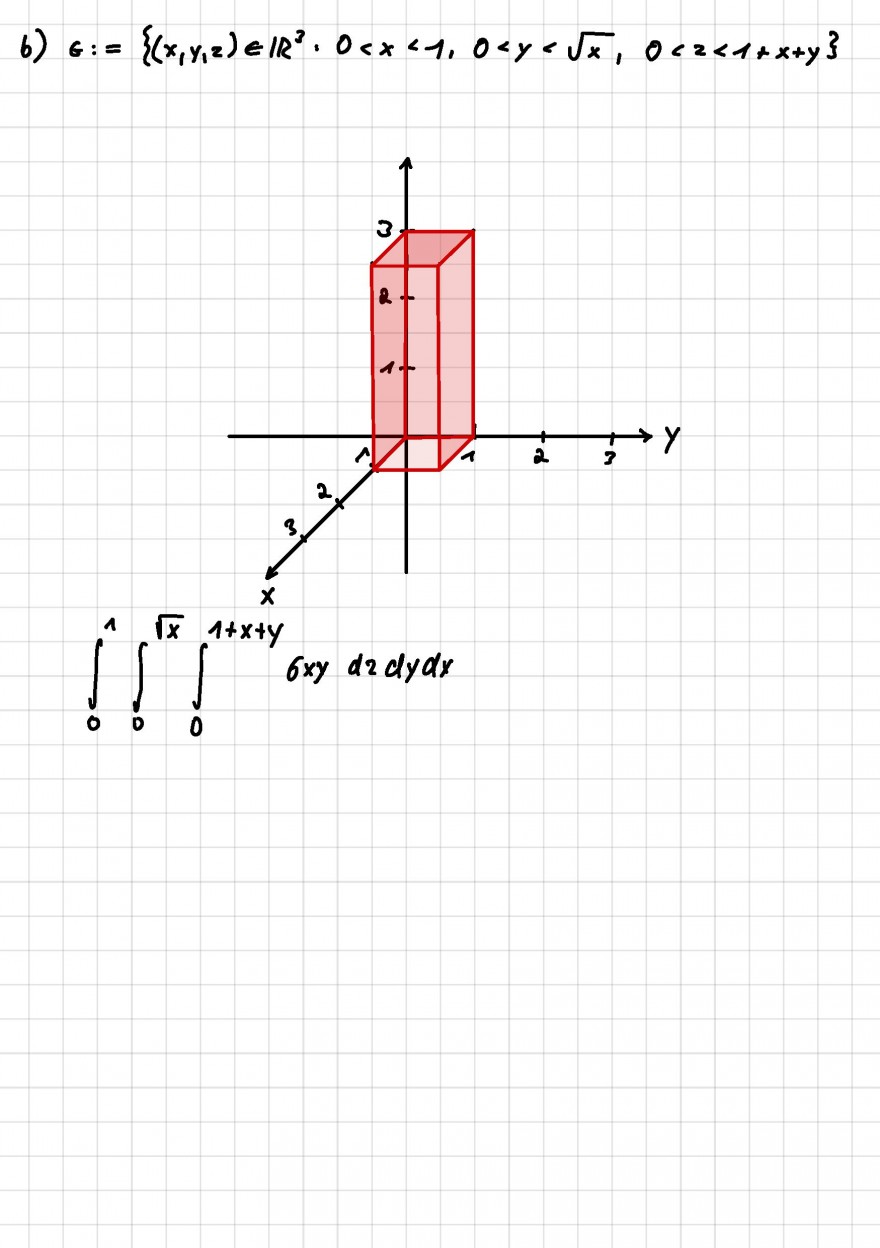
Text erkannt:
b) \( \boldsymbol{G}:=\left\{\left(x, y_{1} 2\right) \in \mathbb{R}^{3} \cdot 0<x<1,0<y<\sqrt{x}, 0<2<1+x+y\right\} \)
\( \int \limits_{0}^{1} \int \limits_{0}^{\sqrt{x}} \int \limits_{0}^{1+x+y} 6 x y d 2 d y d x \)
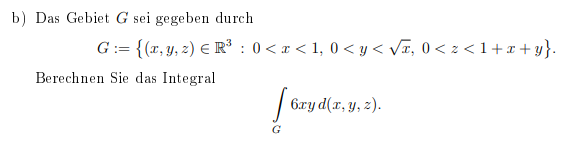
Text erkannt:
b) Das Gebiet \( G \) sei gegeben durch
$$ G:=\left\{(x, y, z) \in \mathbb{R}^{3}: 0<x<1,0<y<\sqrt{x}, 0<z<1+x+y\right\} . $$
Berechnen Sie das Integral
$$ \int \limits_{G} 6 x y d(x, y, z) $$
Problem/Ansatz:
Hallo alle zusammen!
Ich habe ein Problem damit die Grenzen des Gebiets hier festzulegen bzw. die Integrationsgrenzen.
Ich habe versucht mir das Gebiet erstmal zu skizzieren und bin mit folgenden gedankengängen zu dem ergebnis gekommen welches ihr oben seht.
- ich habe x von 0 bis 1 erstmal eingezeichnet
- dann habe ich für 0 < y < \( \sqrt{x} \) ebenfalls von 0 bis 1 angenommen, da x ja auch von 0 bis 1 eingegrenzt ist.
- für z habe ich dann von 0 bis 3, da ich für x und y jeweils 1 angenommen habe, jedoch bin ich mir nicht sicher weil diese ja kleiner als 1 sein sollen sprich meine behauptung kann auch gut und gern falsch sein.
Wie gehe ich hier vor habt ihr eine Lösung und vielleicht generelle tipps zum vorgehen in solchen aufgaben?
Vielen dank im voraus und Liebe Grüße!