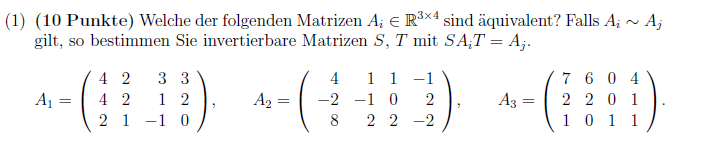
Text erkannt:
(1) (10 Punkte) Welche der folgenden Matrizen \( A_{i} \in \mathbb{R}^{3 \times 4} \) sind äquivalent? Falls \( A_{i} \sim A_{j} \) gilt, so bestimmen Sie invertierbare Matrizen \( S, T \) mit \( S A_{i} T=A_{j} \).
\( A_{1}=\left(\begin{array}{rrrr}4 & 2 & 3 & 3 \\ 4 & 2 & 1 & 2 \\ 2 & 1 & -1 & 0\end{array}\right), \quad A_{2}=\left(\begin{array}{rrrr}4 & 1 & 1 & -1 \\ -2 & -1 & 0 & 2 \\ 8 & 2 & 2 & -2\end{array}\right), \quad A_{3}=\left(\begin{array}{cccc}7 & 6 & 0 & 4 \\ 2 & 2 & 0 & 1 \\ 1 & 0 & 1 & 1\end{array}\right) \)
wie berechnen die Matrizen S,T? ich habe schon gewusst,dass A1 und A3 äquvalenz sind