Hallo Hallo,
Zu ermitteln ist eine Abbildungsmatrix (2x2). ... Mithilfe der Standardeinheitsvektoren
Die Einheitsvektoren hast Du schon erwähnt $$e_1= \begin{pmatrix}1\\ 0\end{pmatrix}, \quad e_2= \begin{pmatrix}0\\ 1\end{pmatrix}$$dann drehe doch mal \(e_1\) um einen Winkel \(\alpha\) (hier blau)

Dann wird aus \(e_1\) der Vektor \(e'_1\) und dessen Koordinaten kann man aus der Zeichnung ablesen$$e'_1 = \begin{pmatrix} \cos \alpha\\ \sin \alpha\end{pmatrix}$$wenn es nun eine Drehmatrix \(R\) geben soll, die \(e_1\) nach \(e'_1\) transformiert, dann muss doch da stehen$$\begin{aligned}e'_1 &= R \cdot e_1 \\ \begin{pmatrix} \cos \alpha\\ \sin \alpha\end{pmatrix} &= \underbrace{\begin{pmatrix} \cos \alpha & ?\\ \sin \alpha& ?\end{pmatrix}}_{=R} \cdot \begin{pmatrix}1\\ 0\end{pmatrix}\end{aligned}$$Durch die Multiplikation mit \(e_1\) wird doch die erste Spalte von \(R\) als Ergebnis übernommen. Umgekehrt heißt dass, dass die erste Spalte von \(R\) gleich \(e'_1\) sein muss.
Überlege Dir das gleiche (mit Skizze!) für die zweite Koordinatenrichtung \(e_2\). Das Ergebnis ist$$R = \begin{pmatrix} \cos \alpha & -\sin \alpha\\ \sin \alpha& \cos \alpha\end{pmatrix}$$
Spiegelung an einer Ursprungsgeraden mit Winkel Beta gegen die X-Achse
Gesucht ist also eine Spiegelmatrix \(S_{\beta}\). Hilfreich ist, wenn man weiß, dass man eine Rotation um \(\alpha\) durch zwei Spiegelungen ersetzen kann. Wobei die Spiegelachsen frei wählbar sind, die Achsen müssen nur den Winkel \(\alpha/2\) gegeneinander einnehmen. Mache Dir mal eine Skizze und probiere es mal aus.
Die Idee ist, dass es eine Rotation um den Winkel \(2\beta\) ergibt, wenn man zwei Spiegelungen hintereinander ausführt$$S_{\beta} \cdot S_0 = R_{2\beta}$$Das \(S_0\) ist eine Spiegelung an einer Geraden mit dem Winkel 0 zur X-Achse, heißt an der X-Achse selbst, und das ist einfach$$S_0 = \begin{pmatrix}1& 0\\ 0& -1\end{pmatrix}$$Falls Dir das nicht klar ist, zeichne Dir die Vektoren \(e_1\) und \(e_2\), spiegele sie an der X-Achse und trage die Koordinaten ihrer Spiegelbilder in die Matrix \(S_0\) ein.
Weiter ist jede (reine) Spiegelung mit sich selbst invers (logisch oder?). Also gilt \(S_0^{-1} = S_0\). Und daraus folgt schon das \(S_{\beta}\)$$\begin{aligned} S_{\beta} \cdot S_0 &= R_{2\beta} &&|\, \cdot S_0 \\ S_{\beta} &= R_{2\beta} \cdot S_0 \\ &= \begin{pmatrix}\cos(2\beta)& -\sin(2\beta)\\ \sin(2\beta)& \cos(2\beta)\end{pmatrix} \cdot \begin{pmatrix}1& 0\\ 0& -1\end{pmatrix}\\&=\begin{pmatrix}\cos(2\beta)& \sin(2\beta)\\ \sin(2\beta)& -\cos(2\beta)\end{pmatrix}\end{aligned}$$
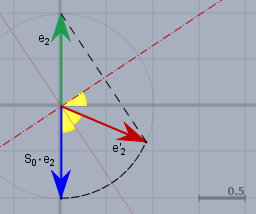
Die Spiegelung von \(S_\beta\) (\(\beta\) ist gelb) wird durch die Spiegelung \(S_0\) an der X-Achse und eine anschließende Drehung \(R_{2\beta}\) erzeugt. Oben als Beispiel mit \(e_2\). Man kann auch hier die Koordinaten von \(e'_2\) aus der Skizze ablesen$$e'_2 = \begin{pmatrix} \sin(2\beta)\\ - \cos(2\beta)\end{pmatrix}$$Vergleiche \(e'_2\) mit der zweiten Spalte von \(S_\beta\) (s.o.)
Bem.: Multiplikationen von Transformationsmatrizen sind in der Form von rechts nach links zu lesen.
4. Drehstreckung
Ist die Kombination einer Drehung und einer Streckung. Die Streckung \(F\) um einen Faktor \(a\) hattest Du schon. Dann kann man auch schreiben$$F_a = \begin{pmatrix}a& 0\\ 0& a\end{pmatrix} = a \cdot E$$wobei \(E\) die Einheitsmatrix ist. Eine Kombination von zwei Transformationen kann durch eine schlichte Multiplikation der Transformationsmatrizen abgebildet werden. Bei Multiplikation von Matrizen ist die Reihenfolge wichtig. Aber da \(E \cdot R = R \cdot E = R\) ist und die Reihenfolge eines Faktors \(a\) bei der Multiplikation irrelevant ist, ist die Drehstreckung \(Z\) um den Winkel \(\alpha\) und den Faktor \(a\)$$Z_{\alpha,\, a} = F_a \cdot R_{\alpha} = a\cdot E \cdot R_{\alpha} = a \cdot R_{\alpha} = \begin{pmatrix} a\cos \alpha & -a\sin \alpha\\ a\sin \alpha& a\cos \alpha\end{pmatrix}$$
Gruß Werner