Berechne die Schnittstelle der Parabel mit der x Achse und ihren Scheitel.Skizziere die Parabel

Question

Aufgabe:

Berechne die Schnittstelle der Parabel mit der x Achse und ihren Scheitel.Skizziere die Parabel
Problem/Ansatz

A) y=x²-4x

B) y=-2x² -8x

Ich bräuchte eine Erklärung wie man das macht da ich dieses Thema nicht so ganz verstehe :)

Answer 1

Hallo,

A)

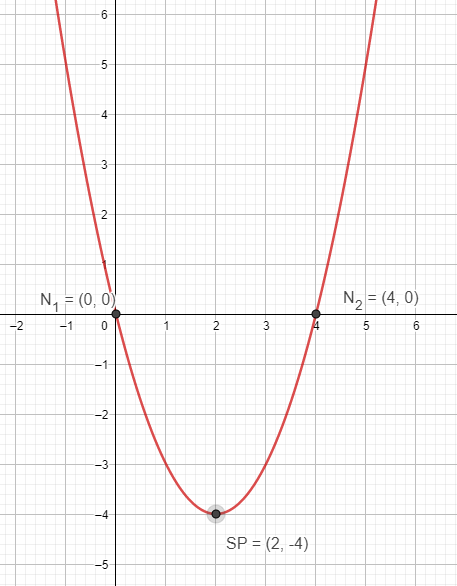
Bestimmung des Scheitelpunktes mit Hilfe der quadratischen Ergänzung:

\( y=x^{2}-4 x \)
\( y=(x-2)^{2}-4 \)

SP \( (2 \mid-4) \)

Berechnung der Nullstellen:

\( x^{2}-4 x=0 \)
\( x\cdot (x-4)=0 \)
\( x=0 \quad \vee \quad x=4 \)

Der Graph sieht so aus:

B kannst du ebenso lösen.

Gruß, Silvia

Answer 2

A) y = x^2 - 4·x = x·(x - 4) = 0

x = 0 oder x = 4

Sx = (0 + 4)/2 = 2

Sy = 2^2 - 4·2 = -4 → S(2 | -4)

B) y = -2·x^2 - 8·x = -2·x·(x + 4) = 0

x = 0 oder x = -4

Sx = (0 + (-4))/2 = -2

Sy = -2·(-2)^2 - 8·(-2) = 8 → S(-2 | 8)

Comments

Die Ermittlung des Scheitelpunkts mithilfe des Mittelwerts der Nullstellen erscheint mir hier deutlich charmanter zu sein als mithilfe der quadratischen Ergänzung.

---

Es ist oft empfehlenswert Aufgaben in der angegebenen Reihenfolge zu bearbeiten. Meist denken sich die Lehrer etwas dabei, wenn in einer Aufgabe zuerst die Nullstellen und dann der Scheitelpunkt bestimmt werden soll.