Gegeben: y=2(x-3)^2-2 und gk=2kx-2+4 verschiedene Aufgaben über Funktion

Question

1. aufgabe
da muss ich scheitelpunkt und wertebereich von funktion f rechen (y=2(x-3)²-2)
ich hab bei den scheitelpunkt S(3|288) ist das richtig? und wie rechne ich den wertebereich?
2.aufgabe 
da muss ich die nullstelle beide funktionen rechnen, 
f(x)=2(x-3)²-2
g_k(x)=2kx-2k+4             bei der funktion g_k muss ich in anhängigkeit auf k rechnen
3. aufgabe
für best. werte d. parameters k ist der zugehörige graph G_gk eine tangente d. Graphens G_f. in diesen fall besitzt G_gk und G_f genau einen gemeinsamen Punkt. Berechne sie diesen werte k

da kam ich überhauptnicht zurecht... und man hat mir einen zwischenergebnis gegeben:
2x²+(-12-2k)x+12+2k=0

ich hoffe auf schnelle hilfe :( ich schreibe morgen SA (ja an einen samstag=... 
 

Answer 1

1. aufgabe 

y = 2·(x - 3)^2 - 2

Da hier die Scheitelpunktform gegeben ist kann man den Scheitelpunkt direkt mit S(3 | -2) ablesen. Da es eine nach oben geöffnete Parabel ist ist der Wertebereich alles ≥ -2. Mach dir mal eine Skizze der Funktion. Der Wertebereich sind die werte die für y heraus kommen können. Kann etwas kleiner -2 heraus kommen und wenn nicht warum nicht?

Comments

2.aufgabe  

f(x) = 2·(x - 3)^2 - 2 = 0

x = 4 ∨ x = 2

gk(x) = 2·k·x - 2·k + 4 = 0

x = (k - 2)/k

---

f(x) = gk(x)

2·(x - 3)^2 - 2 = 2·k·x - 2·k + 4

2·x^2 - 12·x + 16 = 2·k·x - 2·k + 4

2·x^2 - 12·x - 2·k·x + 2·k + 12 = 0

x^2 - 6·x - k·x + k + 6 = 0

x^2 + (- 6 - k)·x + (k + 6) = 0

Diskriminante b^2 - 4*a*c

(- 6 - k)^2 - 4*1*(k + 6) = k^2 + 8·k + 12 = 0
k = -6 ∨ k = -2

Für k = -6 und k = -2 sollte das also eine Tangente sein.

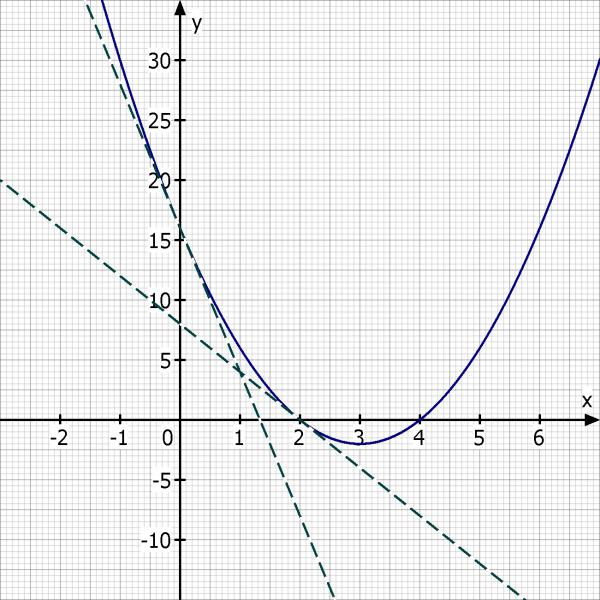
Skizze.