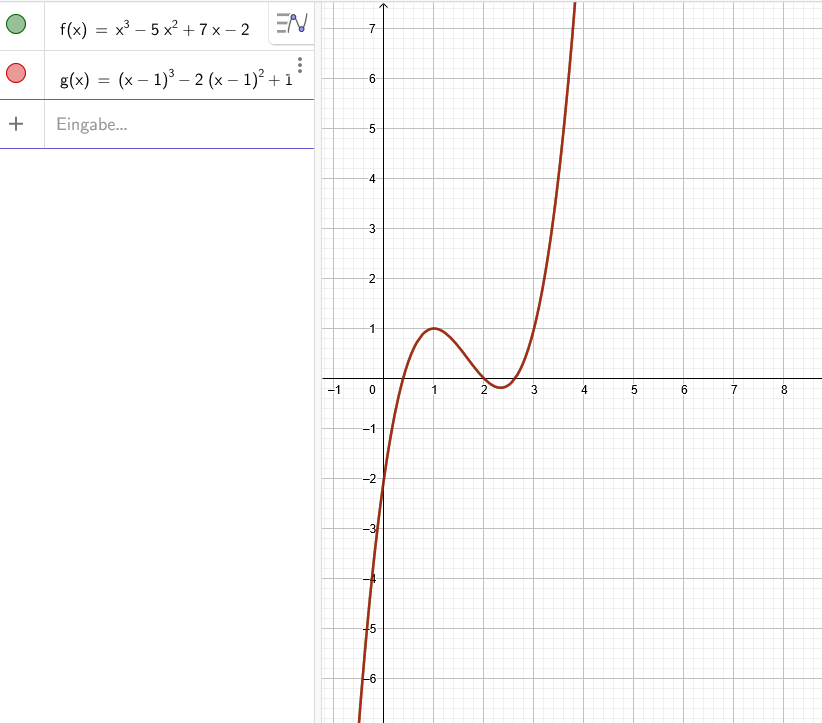
g(x)=x^3-5x^2+7x-2 eine Darstellung der Form g(x)= (x-a)^3-2(x-a)^2+b
x^3-5x^2+7x-2=(x-a)^3-2(x-a)^2+b
x^3-5x^2+7x-2=x^3-3ax^2+3a^2*x-a^3-2*x^2+4ax-2a^2+b
x^3-5x^2+7x-2=x^3-3ax^2-2*x^2+3a^2*x+4ax-a^3-2a^2+b
x^3-5x^2+7x-2=x^3-x^2*(3a+2)+x*(3a^2+4a)-a^3-2a^2+b
Koeffizientenvergleich:
1.)3a+2=5
2.)3a^2+4a=7
3.)-a^3-2a^2+b=-2
a=1 und b=1
g(x)= (x-1)^3-2(x-1)^2+1