Hallo,
Leider haben wir keine Vorgabe bzw. genauere Definition für "Mittelpunkt des Parallelogramms".
Na ja - wenn nicht definiert ist, was 'Mittelpunkt' ist, dann kann man auch nicht zeigen, dass sich die Diagonalen im Mittelpunkt schneiden. Das macht schlicht keinen Sinn.
Du kannst ja definieren, dass der Mittelpunkt eines Parallelogramms dort ist, wo sich die Diagonalen schneiden. Dann wäre die Sache damit erledigt ;-)
Hinweis: Zeigen Sie die Aussage zunächst für ein Quadrat ...
Das finde ich zunächst wenig zielführend! Wichtiger wäre zu wissen, wo sich der Mittelpunkt eines allgemeinen Vierecks befindet! Dazu folgendes:
In einem allgemeinen Viereck fallen mir drei interessante Punkte ein, die irgendwie mittig liegen.
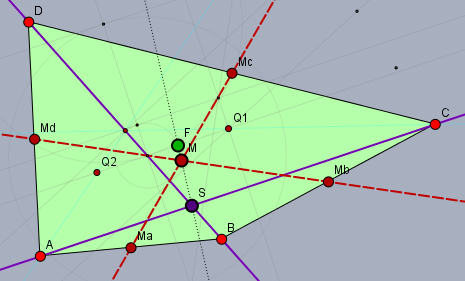
Da ist zunächst mal der Schnittpunkt \(S\) der Diagonalen, sowie der Schnittpunkt \(M\) der Geraden, die durch die gegenüberliegenden Mitten der Seiten gehen. \(M\) ist gleichzeitig der Schwerpunkt der vier Ecken. Und der dritte Punkt \(F\) ist der Schwerpunkt der Fläche des Vierecks. Und im allgemeinen fallen diese nicht zu einem Punkt zusammen (beim Parallelogramm schon!).
... und benutzen Sie für den allgemeinen Fall eine geeignete affine Abbildung.
Ah Ha! wir befinden uns also nicht mehr auf dem 'Standard-Schulniveau'. In diesem Kontext tippe ich mal auf den Punkt \(M\) als Mittelpunkt.
Mit einer affinen Abbildung kann man zwar kein Quadrat auf ein allgemeines Viereck abbilden (schon wegen der Parallelität), aber auf ein Parallelogramm. Sind \(a\), \(b\) und \(d\) die drei Ortsvektoren zu den den Punkten \(A\), \(B\) und \(D\) eines Parallelogramms, so kann ich das Quadrat$$e_1=\begin{pmatrix}0\\ 0\end{pmatrix},\quad e_2=\begin{pmatrix}1\\ 0\end{pmatrix},\quad e_3=\begin{pmatrix}1\\ 1\end{pmatrix},\quad e_4=\begin{pmatrix}1\\ 0\end{pmatrix}$$auf das Parallelogramm abbilden mit$$e'_{1..4} = \begin{pmatrix}b-a& d-a\end{pmatrix} e_{1..4} + a, \quad e'_{1..4}=A,\,B,\,C,\,D$$Wenn ich voraussetze, dass $$M_q= \begin{pmatrix}0,5\\ 0,5\end{pmatrix}$$der Mittelpunkt des Quadrates ist (wäre noch zu zeigen), dann ist der Mittelpunkt \(M_p\) des Parallelogramms ((!)siehe Kommentar unten)$$M_p = \frac12(b-a) + \frac12(d-a) + a = \frac12(b+d)$$und dieser Punkt muss zwangsläufig auf der Diagonalen durch \(B\) und \(D\) liegen. Ein Punkt \(Q\) auf der Diagonalen durch \(A\) und \(C\) lässt sich schreiben als$$ Q = a \lambda+ c(1-\lambda), \quad \lambda \in \mathbb R\\c = b+d-a$$\(c\) sei der Ortsvektor zum Punkt \(C\). Und für \(\lambda=0,5\) erhält man$$Q(\lambda=0,5) = 0,5a+(b+d-a)\cdot 0,5 = \frac12(b+d) = M_p$$Also liegt \(M_p\) auf beiden Diagonalen und ist folglich identisch mit dem Schnittpunkt \(S=M_p\).
Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner