Ich bin darauf gekommen, weil ich so etwas schon einmal gemacht bzw. gesehen habe. Unbefriedigend, klar. Eventuell hilft dir dieser Gedankengang:
Vielleicht kennst du ja komplexe Zahlen und deren Polardarstellung. Oder sogar schon Polarkoordinaten. Da ist die Idee einen Punkt in der Ebene durch seinen Abstand zum Ursprung und einen Winkel zwischen Punkt und x-Achse darzustellen.
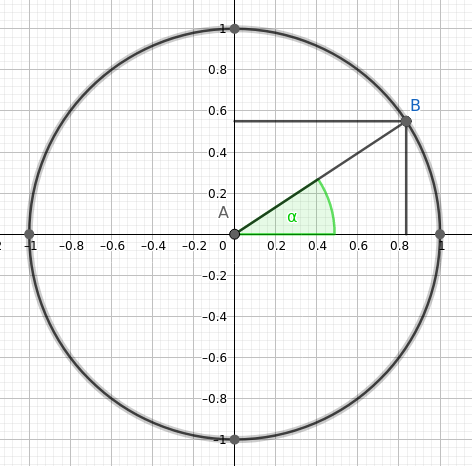
Wie du vielleicht siehst ist der Abstand zum Ursprung für alle Punkte auf dem Kreis r r = 1 und wenn du jetzt den Winkel von 0 bis 2π vergrößerst läufst du den Kreis einmal ab. Und so eine Parametrisierung ist ja nichts anderes wie eine Funktion, die die Kurve abläuft.
Die x-Koordinate von B ist r*cos(α), die y-Koordinate von B ist r*sin(α).
Wenn du also α von 0 bis 2π laufen lässt, läuft der Punkt B(α) = (cos(α),sin(α)) (hier jetzt einfach r=1 einsetzen) den Kreis einmal ab. D.h. du kannst
\( \alpha \mapsto B(\alpha) = (\cos(\alpha), \sin(\alpha)) \)
als Parametrisierung nutzen.