Maximales Volumen aus Kegel

Question

Ich muss bis Montag folgende Aufgabe bewerkstelligen.

skizziere auf ein A4-Blatt (297x210 mm) das Körpernetz eines Kegels in einem Stück, mit dem grösst möglichen Volumen. r,h,s, der Winkel und das Volumen des Kegels, respektive des Körpernetzes müssen auf dem Arbeitsblatt angegeben sein.

Nun habe ich aber wirklich keine Ahnung wie man diese Aufgabe lösen kann, bin leider ziemlich schlecht in Mathe. Würde mich wirklich sehr über eure Hilfe freuen, falls einer von euch weiss wie das geht.

Mit freundlichen Grüssen
nixahnung

Answer 1

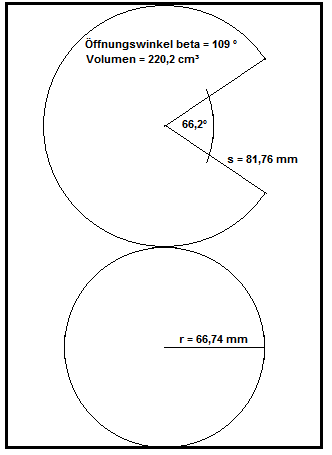
Zunächst die Skizze:

Und wie kommt man darauf?

Ein Kegelnetz ist ein Kreis, aus dem ein Segment ausgeschnitten ist. Rollt man eine solche Figur so zusammen, dass die Schnittlinien s aneinanderstoßen, entsteht ein Kegel. Die Schnittlinien, deren Länge dem Radius des Kegelnetzes entspricht, werden dabei zur Mantellinie des Kegels. Diese ist Hypotenuse des rechteinkligen Dreiecks aus dem Radius r des Kegesl und seiner Höhe h, sodass also nach Pythagoras gilt:

s ² = r ² + h ²

<=> r ² = s ² - h ²

Das Volumen V eines Kegels mit dem Grundflächenradius r und der Höhe h wird nun  berechnet mit der Formel:

V = ( 1 / 3 ) * π * r ² * h

bzw. mit r ² = s ² - h² (siehe oben):

V = ( 1 / 3 ) * π * ( s ² - h ² ) * h

= ( 1 / 3 ) * π * s ² * h  - ( 1 / 3 ) * π * h ³

Das Volumen wird maximal, wenn die Ableitung dieser Formel nach h den Wert 0 annimmt, also:

V ' = ( 1 / 3 ) * π * s ² - π h ² = 0

<=> ( 1 / 3 ) * π * s ² = π h ²

<=> h = √ ( ( 1 / 3 ) * s ² ) = s / √ 3

Also: Ein Kegel hat maximales Volumen eines Kegels wird erreicht, wenn seine Matnelleine √ 3 -mal so lang ist wie seine Höhe.

Für den Radius r des Grundflächenkreises des Kegels gilt dann (siehe oben):

r ² = s ² - h ² = s ² - ( s ² / 3 ) = ( 2 / 3 ) s ²

<=> r = s * √ ( 2 / 3 )

Da der Kreis, aus dem der Kegel gerollt werden soll, möglichst groß sein soll, also an den Rand des DIN A4 - Blattes stoßen soll, kann sein Radius s maximal so groß sein, das dessen doppelter Wert der kleineren Seitenlänge des Blattes  (210 mm ) entspricht, also:

s = 210 / 2 = 105 mm

Damit ergibt sich für den Radius r_max des Grundflächenkreises des Kegels mit maximalem Volumen:

r_max = s * √ ( 2 / 3 ) ≈ 85,7 mm

und für die Höhe h_max dieses Kegels:

h_max = s / √ 3 ≈ 60,6 mm

Sein Volumen V_max beträgt:

V_max = ( 1 / 3 ) * π * r²_max * h_max = ( 1 / 3 ) * π * 85,7 ² * 60,6 ≈ 466082,6 mm³ ≈ 466,1 cm ³

Der Öffnungswinkel beta des Kegels ist das Doppelte des Winkels phi zwischen der Mantellinie s und der Höhe h des Kegels. Für diesen gilt:

sin ( phi ) = r / s

<=> phi = arcsin ( r / s ) = arcsin ( 85,7 / 105 ) =  54,7 °

und somit

beta = 2 * phi = 109,4 °

 

Für die Zeichnung benötigt man noch den Winkel alpha zwischen den beiden Schnittlinien s des herausgeschnittenen Sektors. Dazu überlegt man sich, dass der Umfang u = 2 * π * r des Kegelgrundkreises aus dem Umfang U = 2 * π * s des Kegelnetzes entsteht, in dem man aus U ein Kreisbogenstück der Länge

2 * π * s * alpha / 360 °

herausschneidet. Es gilt also:

u = U - 2 * π * s * alpha / 360 °

<=> 2 * π * r = 2 * π * s - 2 * π * s * alpha / 360 °

<=> r = s - s * alpha / 360 °

<=> r = s ( 1 - alpha / 360 ° )

<=> r / s = 1 - alpha / 360 °

<=> alpha = ( 1 - r / s ) * 360 °

Somit gilt für den Winkel zwischen den Schnittlinien des Kegelnetzes des berechneten Kegels:

alpha = ( 1 - ( 85,7 / 105 ) ) * 360 ° = 66,2 °

 

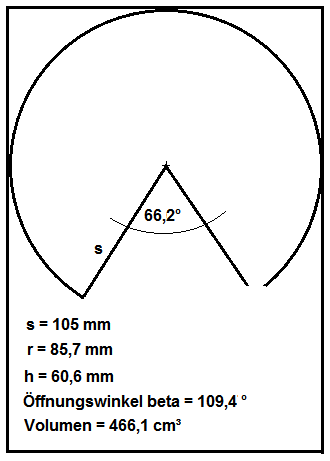
EDIT: Hier die korrigierte Skizze (siehe Kommentare):

Comments

Das ist kein Körpernetz, das ist nur der Mantel. ;)

Davon abgesehen hat der FS Crossposting betrieben und auch schon im MatheBoard Hilfe erhalten.

---

Habe das meiste verstanden. Was ich aber nicht richtig verstehe ist was der "Öffnungswinkel b = 109.4°" bedeutet.

---

Der Öffnungswinkel eines Kegels ist der Winkel, der an der Spitze des Kegels durch zwei sich "gegenüber liegende" Mantellinien des Kegels gebildet wird. Schneidet man einen Kegel so durch, dass der Schnitt durch die Spitze und durch den Mittelpunkt der Grundfläche geht, dann ist dies derjenige Winkel der Schnittfläche, der dort liegt, wo sich die Spitze des Kegels befand.

Der anonyme Kommentator hat allerdings insoweit recht, als ich das Körpernetz ohne die kreisförmige Kegelgrundfläche gezeichnet und berechnet habe. Soll diese Kegelgrundfläche ebenfalls mit auf das Arbeitsblatt, dann müsste sie als Kreis mit dem Radius r in einem Punkte des gezeichneten Mantelkreises an diesen angehängt werden. Die Höhe H dieser Figur ist dann die Summe der Durchmesser beider Kreise, also
H = 2 s + 2 r = 210 + 171,4 = 381,4 mm.
Damit ergibt sich dann das Problem, dass diese nicht mehr unter meine Skizze auf das Arbeitsblatt passt, da dieses nur 297 mm hoch ist.

Zum Glück gibt es eine einfache Lösung dieses Problems:

Man verkürzt die Radien r und s so, dass gilt:

r ' / s ' = r / s = 85,7 / 105 und
2 r ' + 2 s ' = 297

<=>

r ' = 85,7 * s ' / 105 und
r ' = ( 297 - 2 s '  ) / 2

<=>

85,7 * s ' / 105 = ( 297 - 2 s '  ) / 2

<=> 171,4 * s ' = ( 297 - 2 s ' ) * 105

<=> 171,4 * s ' = 297 * 105 - 210 s '

<=> 381,4 s ' = 31185

<=> s ' = 31185 / 381,4 = 81,76 mm

=> r ' = ( 297 - 2 * 81,76  ) / 2 = 66,74 mm

Für die Höhe des Kegels, bei der dieser sein maximales Volumen hat, ergibt sich dadurch

h ' = s ' / √ 3 = 47,20 mm

und das maximale Volumen ist:

V_max = ( 1 / 3 ) * π * r ^{' 2} * h ' = ( 1 / 3 ) * π * 66,74 ² * 47,2 ≈ 220162 mm³ ≈ 220,2 cm ³

Die Winkel alpha = 66,2° und und beta=109,4° bleiben unverändert, da deren Größe nur vom Verhältnis r / s abhängen, welches ja unverändert geblieben ist.

Ich werde sogleich eine neue, korrigierte Zeichnung erstellen und sie in meine Antwort einfügen.