Modellierungsaufgabe, Fehler finden

Question

Aufgabe:

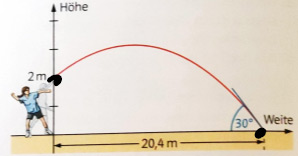
Beim Kugelstoßen beschreibt die Kugel angenähert eine Bahn wie in der Figur dargestellt.

a) Bestimmen Sie eine ganzrationale Funktion, deren Graph den Verlauf der Wurfbahn näherungsweise beschreibt.

b) Berechnen Sie den höchsten Punkt der Flugbahn sowie den Abwurfwinkel (Winkel gegen die Horizontale).

c) In der Regel werden die größten Weiten bei Abwurfwinkeln zwischen \(37^{\circ}\) und \(41^{\circ}\) erzielt. War demnach der Versuch optimal?

Hier komme ich leider nicht weiter:

also als Bedingungen habe ich gegeben:

P1(0|2) P2 (20,4|0) und f´(20,4) = 30° entspricht  tan (a) = m

-> tan(30°) = 0.5774 und aufgrund der Orientierung des Winkels oder der Steigung der Tangenten die ja abfällt muss es -0,5774 sein.

Also mach ich mich daran die Bedingungen in den Ansatz einzusetzen der ax^2 +bx +c ist.

1 Bed: F(0) = 0 + 0 + c = 2 -> c = 2

2 Bed: F(20,4) = a*20,4^2 + b*20,4 +2 = 0

3 Bed: F`(20,4) = -0,5774 -> 2*a*20,4 + b = -0,5774

Jetzt hab ich ein LGS:

I ) a*20,4^2 +20,4 b +2 = 0

II ) 40,8a +b = -0,5774

-> II ) b = -40,8a - 0,5774

II in I einsetzen

I ) a*20,4^2 +20,4*( -40,8a - 0,5774) +2 = 0

auflösen nach a und dann hätte ich a = -0,0235

was aber nicht richtig ist. Kann mir jemand helfen wo was Falsch ist?

Comments

... hätte ich a = -0,0235 was aber nicht richtig ist.

woher weißt Du denn, dass das falsch ist? und was wäre das 'richtige' Ergebnis?

---

Es lag eigentlich nur daran, dass ich dann zu dumm war mein b auszurechnen und mittels dem Punkt P(20,4|0) geschaut habe ob mit dem x- Wert dann 0 rauskommt und weil mein b halt falsch war, war es nie null und da dachte ich immer dass der Fehler bei a liegen müsste, weil b ja nur noch einsetzen ist, aber naja manchmal tuts halt weh :D

Answer 1

W(0|2); N(20,4|0)   f´(20,4)=tan150°

f(x)=a*x^2+b*x+c

W(0|2)

f(0)=c

1.)c=2

f(x)=a*x^2+b*x+2

N(20,4|0)

f(20,4)=a*20,4^2+b*20,4+2

2.)a*20,4^2+b*20,4+2=0

f´(x)=2ax+b

f´(20,4)=2a*20,4+b

3.)2a*20,4+b=tan(150°)=-\( \frac{1}{3} \)*\( \sqrt{3} \)

a≈-0,023 und  b≈0,38

f(x)=-0,023*x^2+0,38*x+2

Comments

Nochmal eine Frage, wieso musste man hier nochmal mit -30° bzw. 150° rechnen und nicht mit den 30? Ich mein im Kopf zu haben, dass da was war mit das Winkel eine Orientierung haben, aber wenn das so ist wie ist dass damit auszulegen?

---

tan(30°)=\( \frac{1}{3} \)*\( \sqrt{3} \) Da bekommst du eine positive Steigung. Sie muss aber negativ sein. Siehe dein Bild.

---

Nochmal eine Frage, wieso musste man hier nochmal mit -30° bzw. 150° rechnen und nicht mit den 30?

Du musst mit \(-30°\) rechnen. Die Steigung ist negativ und die Steigung wird immer von links nach rechts - also zu steigenden X-Werten hin definiert. Weiter gilt, dass \(-\tan 30°=\tan 150°\)

---

danke, für eure ausgiebige Hilfe :D

Answer 2

Hallo,

auflösen nach a und dann hätte ich a = -0,0235
was aber nicht richtig ist. Kann mir jemand helfen wo was Falsch ist?

Da ist gar nichts falsch. Wenn ich Dein Ergebnis einsetze komme ich genau zu dieser Funktion:

~plot~ -0.0234956x^2+0.381272x+2;[[-4|22|-3|12]];{20,4|0};{0|2} ~plot~

$$f(x) = -0,023496x^2 +0,38127x + 2$$so wie sie im Bild oben dargestellt ist. Evt. liegt ein Fehler bei der Aufgabenstellung vor. Der Winkel kommt mir auch recht flach vor. Der Abwurfwinkel ist so nur \(\approx 20,9°\)

Mit \(60°\) statt \(30°\) komme ich zu $$f(x) = -0,08010x^2+1,536x+2$$Gruß Werner

Comments

danke, war sehr hilfreich ^^, vor allem mit dem Schaubild