Aufgabe:
Gegeben sind die Funktionen f und g. Die Graphen der beiden Funktionen schließen eine Fläche mit dem Inhalt A ein.
Welche der folgenden Berechnungsansätze treffen zu? Kreuzen Sie an!
A) \( A=\int \limits_{-2}^{2}[f(x)-g(x)] d x \)
B) \( A=\int \limits_{-2}^{2}[g(x)-f(x)] d x \)
C) \( A=\int \limits_{-2}^{2} g(x) d x-2 \cdot \int \limits_{1}^{2} f(x) d x \)
D) \( A=2 \cdot \int \limits_{0}^{2}[g(x)-f(x)] d x \)
E) \( A=\left|\int \limits_{-2}^{2} f(x) d x\right|+\left|\int \limits_{-2}^{2} g(x) d x\right| \)
B, C und D sind die richtigen - doch was passiert wenn ein Teil der zu berechnenden Fläche im negativen Teil ist? Muss man da nicht irgendwas Subtrahieren oder das Vorzeichen auf negativ stellen?
Die Fläche zwischen den beiden Graphen:
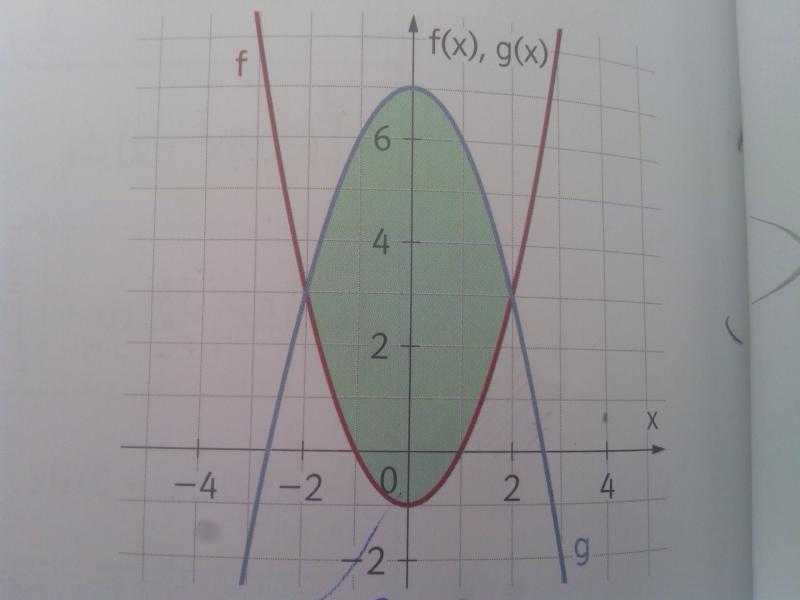
Mein Ansatz:
1. Das erste ist falsch weil man den Oberen Graphen - den Unteren machen muss und weil man auch wenn es g(x)-f(x) macht ein 2* vor dem Integral fehlt weil man nur die eine Hälfte ausrechnet oder?
Bei den restlichen versteh ich es nicht ganz, weil auf der y- Achse ein Teil des grünen Bereiches im negativen ist und ich nicht weiß wie man damit umgehen soll - ganz einfach nicht beachten oder irgendetwas negativ stellen oder Betrag nehmen?
Es wäre nett wenn ihr jedes einzelne beschreibt warum es nicht sein kann bzw. warum das angekreuzte sein kann