Aufgabe
Multiple-Choice-Tests lassen sich einfach auswerten. Wenn n Fragen eines solchen Tests unabhängig sind, lässt sich das Ausfüllen eines Testbogens als Bernoullikette auffassen, wobei die Trefferwahrscheinlichkeit p die „Fachkompetenz" misst. Man besteht den Test, wenn man von den 10 Fragen mindestens 8 richtig beantwortet.
a) Wie groß ist die Wahrscheinlichkeit, dass man bei dem Test
1) besteht, obwohl man keine Ahnung hat und nur zufällig ankreuzt, also „pures Glück hat"?
2) durchfällt, obwohl die Wahrscheinlichkeit, dass man eine Frage richtig beantwortet, 90% beträgt, also „Pech hat"?
b) Was ändert sich bei a), wenn man zum Bestehen 9 Fragen richtig beantworten muss?
=> Bei einem Mathetest gib es 10 Fragen mit jeweils vier Antworten, von denen nur eine richtig ist.
Ansatz
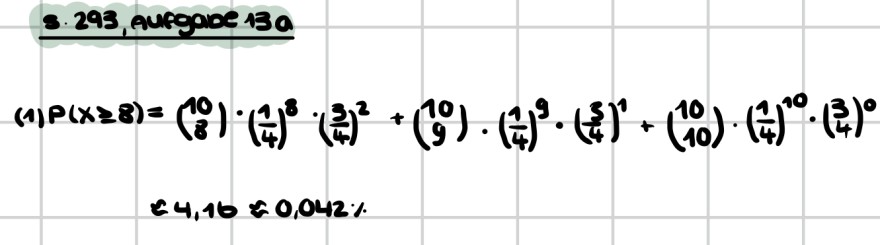
Text erkannt:
3. 293 , aurgade 13 a
\( \begin{aligned} (1) P(x \geqslant 8) & =\binom{10}{8} \cdot\left(\frac{1}{4}\right)^{8} \cdot\left(\frac{3}{4}\right)^{2}+\binom{10}{9} \cdot\left(\frac{1}{4}\right)^{9} \cdot\left(\frac{3}{4}\right)^{1}+\binom{10}{10} \cdot\left(\frac{1}{4}\right)^{10} \cdot\binom{3}{4}^{0} \\ & =4,16 \approx 0,042 \% \end{aligned} \)
Ist die Aufgabe 13a (1) richtig? Und wie kann ich die anderen Aufgaben lösen?