Aufgabe:
Die Produktionskosten (in Euro) eines Betriebs setzen sich aus Fixkosten und den variablen Kosten zusammen, die bei der Produktion von x Einheiten eines Produktes anfallen. Der Erlös(Umsatz) ist der Betrag, der beim Verkauf von x Einheiten eines eingenommen wird, der Gewinn ist die Differenz aus Erlös und Kosten.
In der folgenden Abbildung sind eine Kostenfunktion K, eine Erläsfunktion E und die Gewinnfunktion G dargestellt.
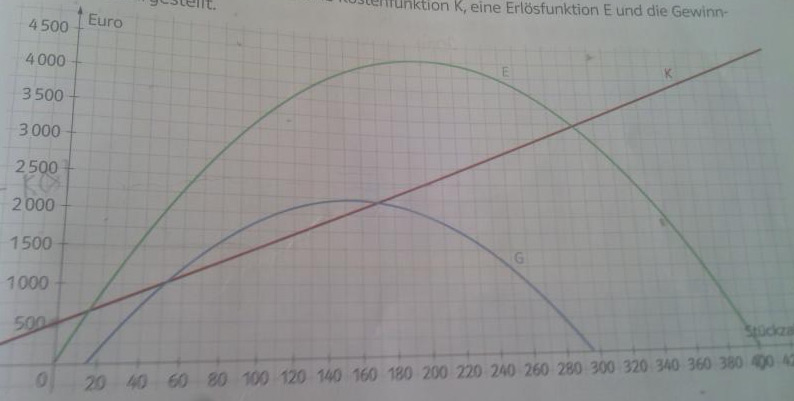
Aufgabenstellung:
b) Ermitteln Sie die Fixkosten sowie die Produktionskosten pro Stück in diesem Betrieb und geben Sie eine Termdarstellung der Kostenfunktion K an!
Hier liegts bei mir eher am Verständnis - Ich hab keinen Schimmer was die mit Fixkosten und Produktionskosten meinen - klingt irgendwie nach dem gleichen
die Funktion von K hab ich schon bestimmt: K(x) = 10x + 500
c)Geben Sie die Zahlen E(0), E(200), E(400) an und intepretieren Sie diese im Kontext.
Was gibt die Stele x an, für die E ' (x) = 0 gilt?
--> Das erste ist irgendwie klar - ganz einfach die Zahlen von E an den Stellen 0,200,400 ablesen und sagen was das ist
beim zweiten weiß ich auch nicht was passiert wenn man die Funktion des Umsatzes ableitet und 0 setzt. Die Funktion wir eben linear und fallend, da E(x) eine Parabel ist
d) Die Funktion E ist näherungsweise eine Polynomenfunktion vom Grad 2. Geben sie Formeln für E(x) und G(x) an und berechnen Sie damit, für welche Stückzahl die Produktion gewinnbringend verläuft! Was könnte man unter dem Gewinnbereich des Betriebes verstehen?
Ich weiß nicht wie man a und b von einer Polynomenfunktion bestimmen soll. Mein einziger Vorschlag wäre Punkte abzulesen - diese in diese Gleichung einsetzen also in -ax^2+bx und diese durch Additionsverfahren und Eliminierung oder Substitution zu lösen - bitte mit Rechenweg angeben.