folgende Aufgabe:
Berechnen Sie die Länge der Windrispe und die Größe des Winkels zwischen Windrispe und Sparren.
Gegeben ist eine Skizze die im Prinzip der eingefügten entspricht
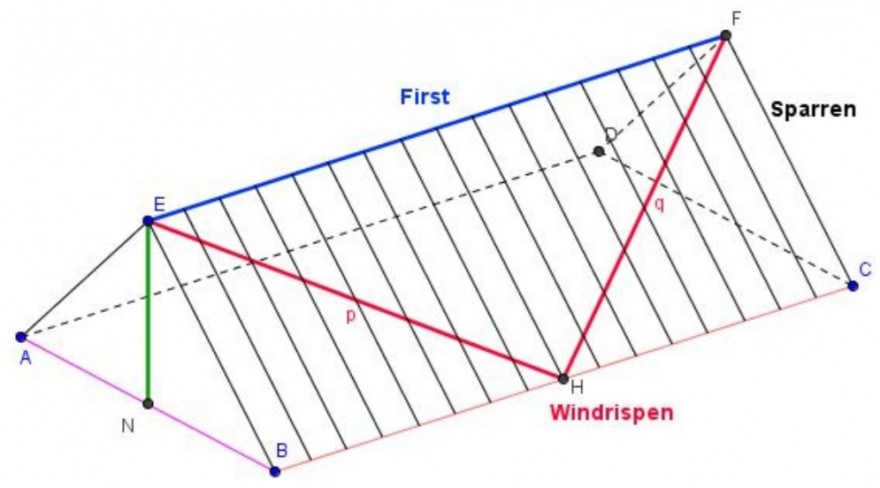
gegeben ist:
AB = 9,00
NE = 3,50
BC = 14,50
(In der folgenden Rechnung habe ich die Punkte anders benannt, das mache ich aber deutlich)
Ansatz:
ich habe erst die Seitenlänge mit dem Satz des Pythagoras berechnet:
s = (4,50^2 + 3,50^2)^0,5 ~ 5,7
und damit dann die Länge der Windrispe, auch mit dem Satz des Pythagoras:
w = (7,25^2 + 5,7^2)^0,5 ~ 9,22
dann habe ich ein 2D Koordinatensystem gezeichnet (und an dieser Stelle bin ich mir auch unsicher, ob ich das so darstellen kann)
und ein rechtwinkliges Dreieck ABC gezeichnet wobei:
A (0/0), B(7,25/0), C (7,25/5,7)
AB -> die untere Kante vom Dach (jedoch nur die Hälfte, liegt auf der x-Achse)
AC -> Windrispe
CB -> Sparren
Den Winkel gamma hab ich dann mit (a und b sind jeweils als Vektoren zu verstehen)
cos(gamma) = a • b / |a| • |b|
berechnet.
(Schreibweise der Koordinaten erfolgt nebeneinander)
a Vektor = CB Vektor = ( 0 ; -5,7)
b Vektor = CA Vektor = ( -7,25 ; 5,7 )
Die Beträge der Vektoren a und b entsprechen ja den schon berechneten Seitenlängen.
Entsprechend erhalte ich für
Cos(gamma) ~ 0,618
gamma ~ 51,81°
Ist die Rechnung korrekt? Wenn nicht, woran hängt es?