Wie lässt sich die Aufgabe lösen

Question

Aufgabe:

Vektoren im Quader

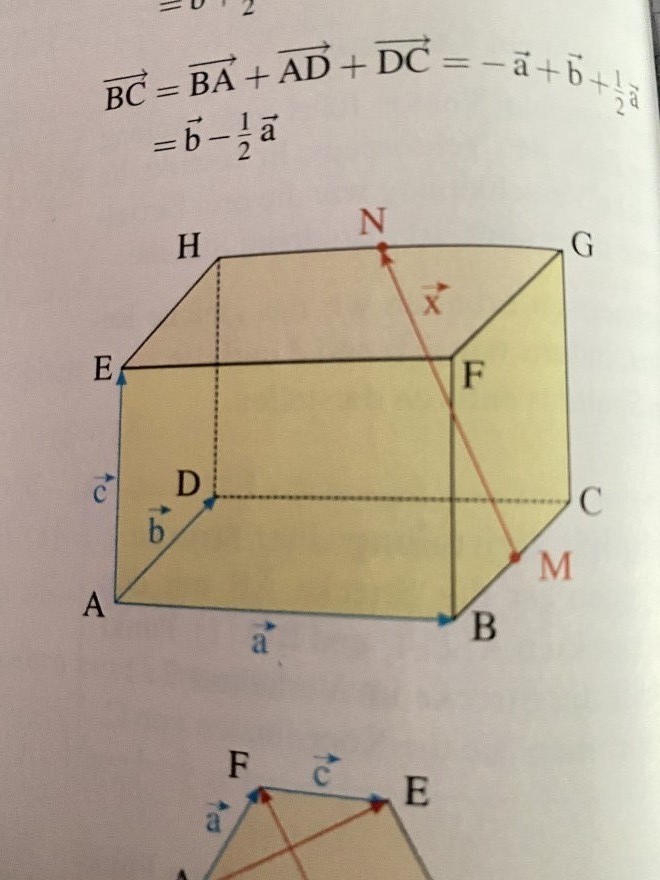
Der abgebildete Quader wird durch die Vektoren a (mit Pfeil), b und c (auch beide mit Pfeil) aufgespannt. Der Vektor x (mit Pfeil) verbindet die Mittelpunkte M und N zweier Quaderkanten.

Stelle den Vektor x (mit Pfeil) mithilfe der aufspannenden Vektoren a (mit Pfeil), b und c ( beide mit Pfeil) dar.

Text erkannt:

\( \overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{BA}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DC}}=-\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\frac{1}{2^{2}} \)
\( =\vec{b}-\frac{1}{2} \vec{a} \)

Problem/Ansatz:

Ich dachte mir, dass man die einzelnen in Wegen nachgehen muss, also Vektoren MB, BA, etc. Dann würde man auf ein Ergebnis von: 1/2 + c - 2 - b - c

Ist das richtig?

Answer 1

M = AM = a + 1/2·b

N = AN = 1/2·a + b + c

x = MN = n - M = (1/2·a + b + c) - (a + 1/2·b) = - 1/2·a + 1/2·b + c

Comments

Vielen vielen Dank! Ich versteh jetzt such meinen Fehler. Die Vektoren gehen immer alphabetisch. Das hatte ich nicht so beachtet und M und N dachte ich müssen zusammengefügt werden und nicht einzeln erstmal ermittelt werden. Wollte erstmal direkt den Vektor MN bestimmen. Danke Ihnen!

---

Du kannst auch MN direkt bestimmen. Dazu gehst du den Weg von M nach N. Ich unterteile dazu den Weg in drei Teile

MC = 1/2·b
CG = c
GN = - 1/2·a

Jetzt fügst du die Teile zusammen

x = MN = MC + CG + GN = 1/2·b + c - 1/2·a = - 1/2·a + 1/2·b + c