Kurvendiskussion mit Parameter: e^{-kx²}

Question

 Ich kann folgende Aufgabe leider nicht lösen. Ich sitze schon seit einer Stunde dran und nichts tut sich. Ich bitte um Hilfe:

Gegeben ist die Funktion f(x) = e^{-kx^2}  mit einem Parameter k ∈ ℝ.  Berechnen Sie in Abhängigkeit von k die lokalen Extrema, Wendestellen einschließlich Wendetangenten (falls vorhanden).

Freundliche Grüße

Comments

Die Gleichung heißt f(x) = e^-kx^2   ein minus fehlte noch. Sorry

Answer 1

Hi

y = e^{-kx^2}
y' = -2kxe^{-kx^2}
y'' = -2ke^{-kx^2} + 4k^2x^2e^{-kx^2} = 2ke^{-kx^2} (2kx^2 - 1)
y''' = -8k^{3}x^{3}e^{-kx^2} + 12k^{2}xe^{-kx^2} = -4k^{2}xe^{-kx^2} (2kx^2-3)

Extrema
y' = 0
-2kxe^{-kx^2} = 0
x = 0 oder k = 0

y''(0) = -2*k*e^{-k*0^2} + 4*k^2*0^2*e^{-k*0^2}
y''(0) = -2k
y''(0) ≠ 0 für x = 0 und k ≠ 0, d.h an der Stelle x = 0
existiert ein Extrempunkt, wenn k ≠ 0 ist.
Für k = 0 geht y = e^{-kx²} über in y = 1.

Wendestellen
y'' = 0
-2ke^{-kx^2} + 4k^2x^2e^{-kx^2} = 0
2ke^{-kx^2} = 4k^2x^2e^{-kx^2}
e^{-kx^2} = 2kx^2e^{-kx^2}
Lösungen:
k = 0
oder
2kx^2 = 1
x = ± 1/√(2k), k ≠ 0
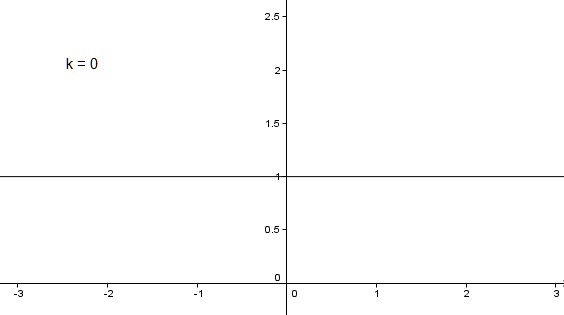
Für k = 0 erhalten wir die Funktion y = 1, das ist eine Gerade parallel zur x-Achse,
diese Funktion hat keine Wendestellen.

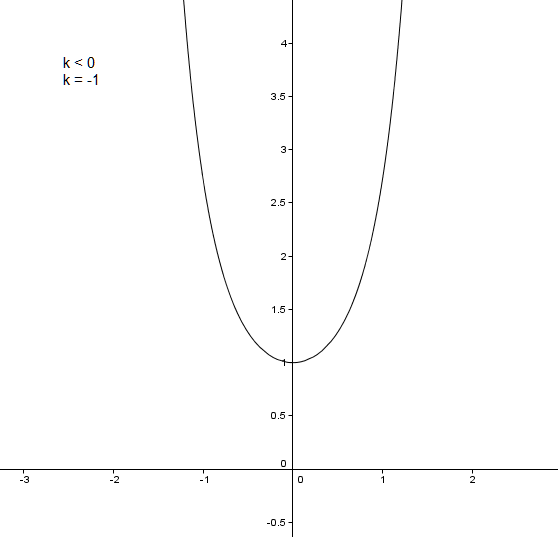
Für k < 0 erhalten wir eine Parabel, die auch keine Wendestellen hat.

 

Hinreichende Bedingung für Wendestelle
y'''(±1/√(2k)) ≠ 0
-8*k^3*(±1/√(2k))^3e^{-k*(±1/√(2k))^2} + 12*k^2*(±1/√(2k))*e^{k*(±1/√(2k))^2} ≠ 0
für k > 0.

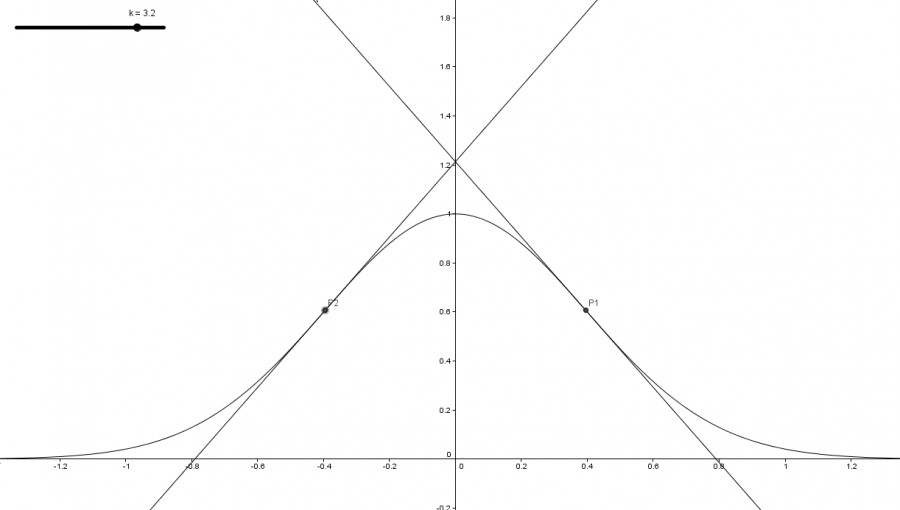
Die Wendestellen sind also x = ± 1/√(2k), k > 0

Wendepunkte
x1 = 1/√(2k)
y1 = e^{-k*(1/√(2k))^2}
y1 = 1/√e
P1(1/√(2k), 1/√e)
x2 = -1/√(2k)
y2 = e^{-k*(-1/√(2k))^2}
y2 = 1/√e
P2(-1/√(2k), 1/√e)

Wendetangenten
1)
y = mx + b
m = f'(1/√(2k)) = -2*k*(1/√(2k))*e^{-k(1/√(2k))^2}
m = -√(2/e) √k
y = 1/√e
x = 1/√(2k)
b = y - mx
b = 1/√e + √(2/e)*√k*1/√(2k)
b = 2/√e
2)
y = mx + b
m = f'(-1/√(2k)) = -2*k*(-1/√(2k))*e^{-k(-1/√(2k))^2}
m = √(2/e) √k
y = 1/√e
x = -1/√(2k)
b = y - mx
b = 1/√e - √(2/e)*√k*(-1/√(2k))
b = 2/√e

T(x) = ±√(2/e)√(k)x + 2/√(e)

k > 0