Zu welcher Uhrzeit bläst Elise die drei Kerzen aus?

Question

Aufgabe:

Problem/Ansatz:

Um 17 Uhr zündet Elise gleichzeitig drei Kerzen an. Sie sind alle drei gleich hoch, aber unterschiedlich dick. Jede Kerze brennt gleichmäßig ab. Um vollständig abzubrennen, braucht die erste Kerze 10 Stunden, die zweite Kerze 8 Stunden und die dritte Kerze 12 Stunden.

Als Elise alle drei Kerzen ausbläst, ist die erste noch genau doppelt so hoch wie die zweite.
a) Zu welcher Uhrzeit bläst Elise die drei Kerzen aus?
b) Ermittle, wie hoch dann die zweite Kerze im Verhältnis zur dritten ist.

Comments

Aufgabe 610812 aus der 61. Mathematik-Olympiade.

Da die Schulrunde bereits beendet ist, kann die Aufgabe und Lösungen offen bleiben.

Answer 1

Sie sind alle drei gleich hoch

Die Höhe ist nicht gegeben, also verwendet man eine Variable: \(h_0\).

Um vollständig abzubrennen, braucht die erste Kerze 10 Stunden

Dann brennt sie pro Stunde um die Höhe \(\frac{h_0}{10}\) ab.

Nach \(t\) Stunden hat sie deshalb die Höhe

        \(h_1(t) = h_0 - \frac{h_0}{10}\cdot t\).

Stelle solche Gleichungen auch für die Höhe der zweiten Kerze \(h_2(t)\) und die Höhe der dritten Kerze \(h_3(t)\) auf.

Als Elise alle drei Kerzen ausbläst, ist die erste noch genau doppelt so hoch wie die zweite.

Zu dem Zeitpunkt ist

(1)        \(h_1(t) = 2\cdot h_2(t)\).

a) Zu welcher Uhrzeit bläst Elise die drei Kerzen aus?

Löse Gleichung (1).

b) Ermittle, wie hoch dann die zweite Kerze im Verhältnis zur dritten ist.

Berechne \(\frac{h_2(t_{\mathrm{aus}})}{h_3(t_{\mathrm{aus}})}\). Ersetze dabei \(t_\mathrm{aus}\) durch die Lösung aus Teilaufgabe a).

Answer 2

Da die Höhe nicht gegeben ist und keine Rolle spielt, kann man sie beliebig wählen.

Sei h=24cm, x,y,z die Höhen der Kerzen beim Ausblasen.

Kerze 1: x=24-2,4t

Kerze 2: y=24-3t

Kerze 3: z=24-2t

x=2y → 24-2,4t=48-6t → 3,6t=24 --> t=20/3

20/3 Std = 6 Std 40 Min

y=24-20=4=12/3

z=24-40/3=32/3

y:z=12:32=3:8

:-)

Comments

Alles klar. Danke dir. :)

---

Was genau bedeutet das t hinter den Zahlen

---

t steht für Zeit (Englisch time) in Stunden.

:-)

Answer 3

a)

a(x) = h - h/10·x
b(x) = h - h/8·x
c(c) = h - h/12·x

Die Gleichung

(h - h/10·x) = 2·(h - h/8·x) --> x = 20/3 = 6 h 40 min

Um 23:40 bläst Elise die Kerzen aus.

b)

(h - h/8·(20/3))/(h - h/12·(20/3)) = 3/8

Die zweite Kerze hat dann nur noch 3/8 der Höhe der dritten Kerze.

Answer 4

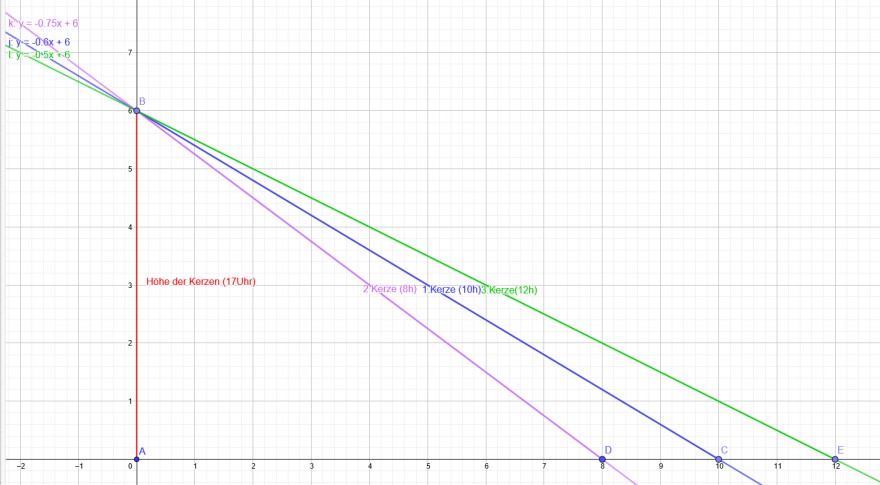
Geradengleichung 1.Kerze: f(x)=-\( \frac{6}{10} \) x+6

Geradengleichung 2.Kerze: g(x)=-\( \frac{3}{4} \) x+6

Geradengleichung 3.Kerze: h(x)=-\( \frac{1}{2} \) x+6

"Als Elise alle drei Kerzen ausbläst, ist die erste noch genau doppelt so hoch wie die zweite."

2*g(x)=f(x)

2*(-\( \frac{3}{4} \) x+6)=-\( \frac{6}{10} \) x+6|:2

-\( \frac{3}{4} \) x+6=-\( \frac{3}{10} \) x+3

x=\( \frac{20}{3} \)

\( \frac{20}{3} \)Stunden=6Stunden und 40 Minuten

a) Zu welcher Uhrzeit bläst Elise die drei Kerzen aus?

Uhrzeit:...

Comments

Wie kommst du auf deine Geradengleichungen?

---

Wie kommst du auf deine Geradengleichungen?

Hier würde eine Anfangshöhe von 6 LE angenommen. Ich habe dort einfach eine Anfangshöhe h genommen. Man kann aber auch 1 LE für 100% nehmen.