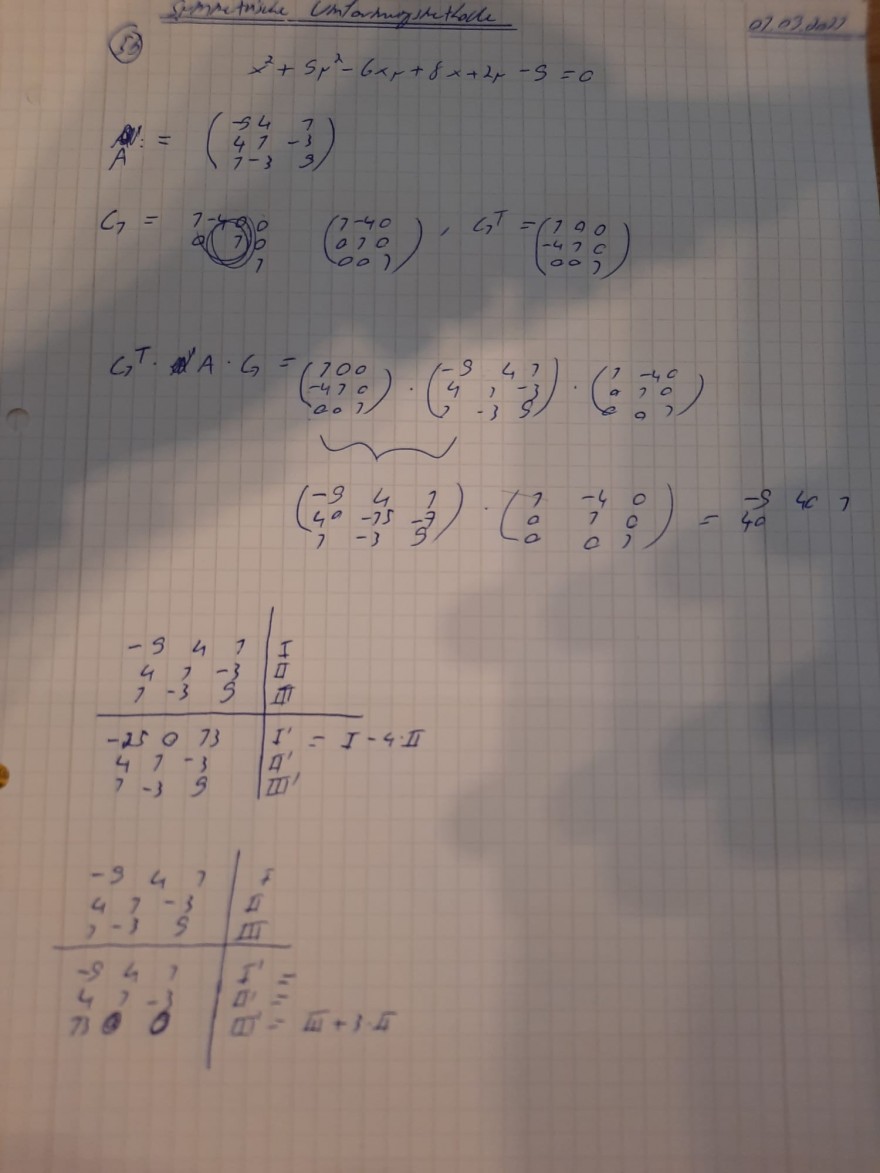symmterische Umformungsmethode, Hauptachsentransformation, Diagonalmatrix

Question

Aufgabe:

Hallo,

ich habe gerade richtig Probleme, die symmetrische Umformungsmethode zu verstehen.

Diese benutzt man ja, um eine Diagonalmatrix zu erstellen.

bei der Matrix A := ((-9,4,1), (4,1,-3), (1,-3,9)).

Problem/Ansatz:

Bei der Lösung die uns vorliegt, wurde als C1 die Matrix ((1,0,0), (0,1,3), (0,0,1) gewählt, mit c1T = ((1,0,0), (0,1,0),(0,3,1)).

Siehe das Bild was ich angehängt habe. Wieso aber kann ich nicht C1 = ((1,-4,0), (0,1,0), (0,0,1)) wählen? Da kommt dann immer was raus, was mir nicht weiterhilft.

Folgende Formel wurde benutzt: C1T * A * C1

Answer 1

Von einer "symmetrische Umformungsmethode"

hab im Zusammenhang mit einer HAT noch nichts gehört:

Allgemein macht man aus der Quadrik, wenn der krakel bei y^2 eine 9 ist?

eine Matrixgleichung

\({\left(\begin{array}{ll}x&y \\ \end{array}\right)}{\left(\begin{array}{rr}1&-3 \\ -3&9 \\ \end{array}\right)}{\left(\begin{array}{l}x \\ y \\ \end{array}\right)}+{\left(\begin{array}{ll}8&2 \\ \end{array}\right)}{\left(\begin{array}{l}x \\ y \\ \end{array}\right)}=9\)

Sucht die Eigenwerte\Eigenvektoren macht eine Drehmatrix draus und verschiebt das achsenparallele Ergebnis in den Ursprung....dann kommt man etwa auf

\(x^{2} + \frac{13}{50} \; \sqrt{10} \; y = \frac{901}{1000}\)

eine Parabel(Gerade)

wie hier z.B:

https://www.geogebra.org/m/jybmgrce

Comments

Danke, aber in der Klausur wird genau diese "symmetrische Umformungsmethode" gefordert.

Man bestimmt ein (mehrere) C mit Gauss, um die Nullen in A zu produzieren, bis nur noch Werte auf der Diagonalen existieren. Dann transponiert man C auch, und wendet dann die von mir genannte Formel an.

Der zweite Schritt wäre dann die selbe Formel mit einem ausgewählten C2, aber das A in der Mitte wäre dann das Ergebnis von der ersten Formel.

Es geht explizit um folgende Frage: Wieso erzeugt die Multiplikation mit dem einen C1 (mit 3) nullen in A, und mit dem anderen C1 (mit -4) keine, obwohl beide laut Gauss-Algorithmus nullen erzeugen?

---

Dann mußt Du warten, bis jemand damit was anfangen kann.

Deine Matrix A sieht falsch aus...

Ich vermute, dass die von mir genannte GLeichung in homogenen Koordinaten angegeben wird - damit müßte die Matrix in meiner Gleichung links oben stehen und die Translation aus den (8,2) rechts und unten?

Ach,

zu Elementarmatrizen und Gauß

https://www.geogebra.org/m/qbtj5mhd

---

Also A kommt daraus zu stande, dass man die erweiterte Matrix (3x3) nennen soll, die die Quadrik x^2 + 9y^2... = 0 beschreibt.

A ist laut verfügbaren Lösungen richtig, denn sie setzt sich wie folgt zusammen:

oben links die Variable -9, rechts und drunter davon der x^1 Wert, jeweils geteilt durch zwei, rechts eins weiter der y^1 wert geteilt durch 2, links ein weiter unten das selbe, und dann die innere 2x2 matrix entsteht durch die x^2, y^2 und x*y werte.

---

Nach dem was ich nachgelesen habe ist die flasch

https://de.wikipedia.org/wiki/Quadrik#Matrixdarstellung

\( Q=\left\{x \in \mathbb{R}^{n} \mid x^{T} A x+2 b^{T} x+c=0\right\} \)

erweiterte Matrix

\( \bar{A}=\left(\begin{array}{cc}A & b \\ b^{T} & c\end{array}\right) \)

---

Die Quadrik die du angegeben hast, beinhaltet nur eine Variable, nämlich x. Die von meinem Beispiel hat x y. Macht das vielleicht einen Unterschied?

Naja, die Matrix ist halt in der Musterlösung der Altklausur angegeben... Wäre komisch, wenn sie falsch wäre.

---

x ∈ Rⁿ
x ∈ R² ==> (x,y)

Ich korrigiere, nicht flasch, sondern auf dem Kopfe stehend - A rechts unten und b,c links und oben....

---

Wie müsste Sie denn deiner Meinung nach richtig aussehen? Bin etwas verwirrt.

---

Ich hab die Antwort... wenn ich die 4 weghaben möchte, dann muss ich C1 so wählen:

((1 0 0), (4/9 1 0), (0, 0,1)), denn 4/9 * -9 + 1 * 4 ergibt 0.

---

Ich kenne das Verfahren nicht.

Siehe Link zu Elementarmatrizen

Meinst Du

\(\small \left\{ \left(\begin{array}{rrr}9&4&0\\4&1&\frac{-31}{9}\\0&\frac{-31}{9}&\frac{80}{9}\\\end{array}\right)= \left(\begin{array}{rrr}1&0&0\\0&1&0\\\frac{-1}{9}&0&1\\\end{array}\right), \left(\begin{array}{rrr}9&4&1\\4&1&-3\\1&-3&9\\\end{array}\right), \left(\begin{array}{rrr}1&0&\frac{-1}{9}\\0&1&0\\0&0&1\\\end{array}\right) \right\} \)

\(\small \left\{ \left(\begin{array}{rrr}9&0&0\\0&\frac{-7}{9}&\frac{-31}{9}\\0&\frac{-31}{9}&\frac{80}{9}\\\end{array}\right)= \left(\begin{array}{rrr}1&0&0\\\frac{-4}{9}&1&0\\\frac{-1}{9}&0&1\\\end{array}\right), \left(\begin{array}{rrr}9&4&1\\4&1&-3\\1&-3&9\\\end{array}\right), \left(\begin{array}{rrr}1&\frac{-4}{9}&\frac{-1}{9}\\0&1&0\\0&0&1\\\end{array}\right) \right\} \)

\(\small \left\{ \left(\begin{array}{rrr}9&0&0\\0&\frac{-7}{9}&0\\0&0&\frac{169}{7}\\\end{array}\right)= \left(\begin{array}{rrr}1&0&0\\\frac{-4}{9}&1&0\\\frac{13}{7}&\frac{-31}{7}&1\\\end{array}\right), \left(\begin{array}{rrr}9&4&1\\4&1&-3\\1&-3&9\\\end{array}\right), \left(\begin{array}{rrr}1&\frac{-4}{9}&\frac{13}{7}\\0&1&\frac{-31}{7}\\0&0&1\\\end{array}\right) \right\} \)

---

\( \begin{pmatrix} 1 & 0 & 0 \\ 4/9 & 1 &0 \\ 0 & 0 & 1 \end{pmatrix} \) * \( \begin{pmatrix} -9 & 4 & 1 \\ 4 & 1 & 3 \\ 1 & -3 & 9 \end{pmatrix} \) * \( \begin{pmatrix} 1 & 4/9 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \)  = \( \begin{pmatrix} -9 & 4 & 1 \\ 0 & 25/9 &-23/9 \\ 1 & -3 & 9 \end{pmatrix} \) * \( \begin{pmatrix} 1 & 4/9 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \) = \( \begin{pmatrix} -9 & 0 & 1 \\ 0 & 25/9 & -23/9 \\ 1 & -23/9 & 9 \end{pmatrix} \)

So, das war der erste Schritt. Wie zu sehen ist, sind die 4er aus A jetzt zu einer 0 geworden. Beim nächsten Schritt brauchen wir eine neue Matrix C, sodass, wenn wir A mit diese und C Transponiert multiplizieren, auch noch die restlichen Werte verschwinden. Da muss ich morgen nochmal draufschauen...

Sorry, ich hätte erwähnen sollen, dass am Ende eine Diagonalmatrix der Form

\( \begin{pmatrix} 0 & 0 & * \\ 0 & * & 0 \\ * & 0 & 0 \end{pmatrix} \) rauskommen soll.