Question

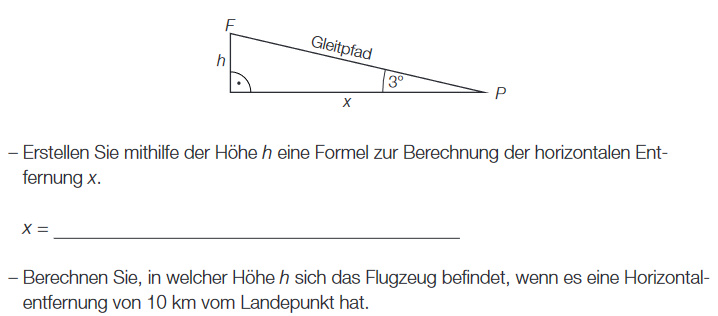
Berechnen Sie, in welcher Höhe h sich das Flugzeug befindet, wenn es eine Horizontalentfernung von 10 km vom Landepunkt hat (Trigonometrie im rechtwinkeligen Dreieck)

Warum nimmt man hier (laut Lösung) den Tangens? Die gesuchte Höhe h ist ja die Gegenkathete. Die gegebene Horizontalentfernung von 10 km ist dann die Hypotenuse. Somit braucht man ja einen Satz, wo die Hypotenuse und die Gegenkathete dabei sind, das wäre in dem Fall der Sinus.

Wenn ich das aber mit dem Sinus berechne, komme ich auf ein anderes Ergebnis..

Answer 1

Für x=10 km errechnet sich h (in km)  aus der Gleichung tan(3°)=\( \frac{h}{10} \).

Comments

Aber wenn man in diese Gleichung einsetzt, würde es ja bedeuten, dass die 10 km die Ankathete wären. Weil der Tangens ist ja Gegenkathete/Ankathete. Aber in dem Fall sind ja die 10 km die Hypotenuse und nicht die Ankathete.

---

Dein Aufgabentext: "Horizontalentfernung von 10 km".

---

Ah okay, das heißt die Variable x sind die 10 km. Habe das falsch gedeutet und geglaubt, wo Gleitpfad steht, das sind die 10 km..

Aber wenn der Gleitpfad die 10 km wären, sprich die Hypotenuse, müsste man das mit dem Sinus berechnen oder?

---

Ja, wenn der Gleitpfad die 10 km wären, sprich die Hypotenuse, müsste man das mit dem Sinus berechnen.

---

Danke, Roland! Lesen sollte man können..

Answer 2

tan(3°) ist definiert aus dem Seitenverhältnis von Gegenkathete h durch Ankathete x = 10 km.

Damit ist in der Formel nur die Unbekannte h zu der Du auflösen kannst

tan(3°) = h/10
h = 10 * tan(3°) = 0.5241 km = 524.1 m

Aber in dem Fall sind ja die 10 km die Hypotenuse und nicht die Ankathete.

Beachte das die Hypotenuse die längste Seite ist, die dem rechten Winkel gegenüber liegt. Das wäre hier der Gleitpfad. Du kannst an der Skizze aber sehen wo die horizontale Entfernung x eingezeichnet ist. Das ist die Ankathete.

Comments

Danke, eigentlich eh ein einfaches Beispiel, habe nur falsch gelesen