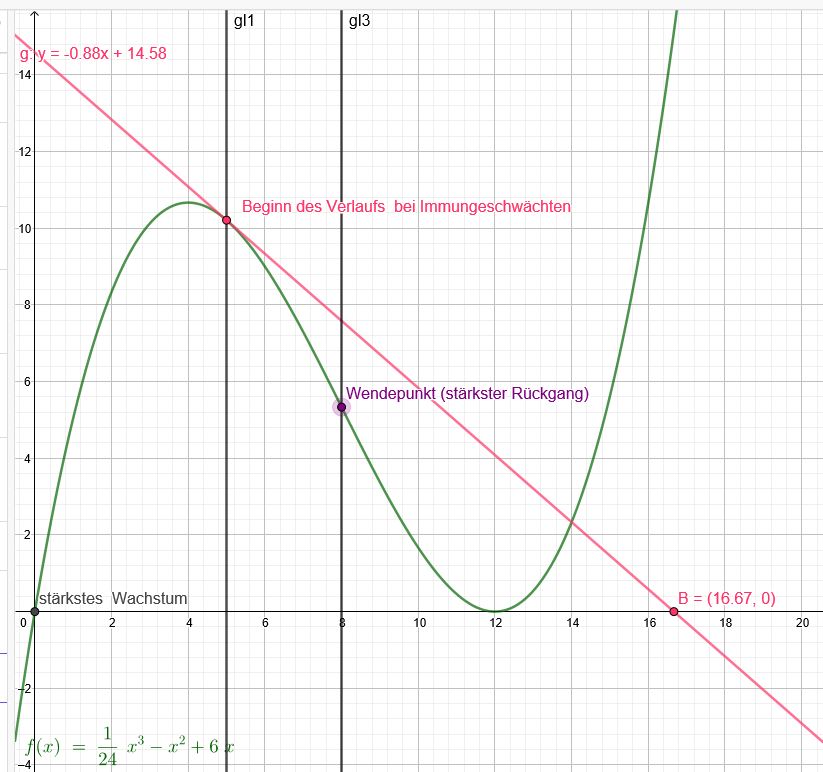
p(t)=\( \frac{1}{24} \) t³-t² + 6t
a) Berechne, wie viele Tage eine Windpockenerkrankung dauert, also wie viele Tage aktive Bläschen im Gesicht des Erkrankten feststellbar sind:
\( \frac{1}{24} \) t³-t² + 6t=0
t*(\( \frac{1}{24} \) t^2-t+6)=0
t₁=0
\( \frac{1}{24} \) ≈t^2-t+6=0
t=12
b) Ermittle rechnerisch, an welchem Tag nach Ausbruch der Krankheit die meisten Bläschen im Gesicht eines Erkrankten zu beobachten sind. Gib auch die Anzahl an.
p´(t)=\( \frac{1}{8} \) t^2-2t+ 6
\( \frac{1}{8} \) t^2-2t+ 6=0
t₁=4 p(4)=\( \frac{1}{24} \) *4³-4² + 6*4=\( \frac{32}{3} \) =10 \( \frac{2}{3} \)
t₂=12 ( war schon Nullstelle, somit Minimum.)
c) Ermittle ebenfalls rechnerisch, zu welchem Zeitpunkt der größte Zuwachs an Bläschen zu erwarten ist
t₁=0 p´(0)= 6
und an welchem Tag die Anzahl der aktiven Bläschen am stärksten abnimmt.
p´´(t)=\( \frac{1}{4} \) t-2
\( \frac{1}{4} \) t-2=0
t=8 Wendepunkt
d) Bei immungeschwächten Kindern verläuft die Krankheit ab dem fünften Tag annähernd linear. Ermittle, an welchem Tag dann erstmals keine aktiven Papeln mehr feststellbar sind.
p(5)=\( \frac{1}{24} \) *5³-5² + 6*5=\( \frac{245}{24} \)
p´(5)=\( \frac{1}{8} \)* 5^2-2*5+ 6=-\( \frac{7}{8} \)
Allgemeine Geradengleichung: \( \frac{y-y₁}{x-x₁} \)=m

Text erkannt:
$$ \begin{array}{l} \frac{p(t)-\frac{245}{24}}{t-5}=-\frac{7}{8} \\ p(t)-\frac{245}{24}=-\frac{7}{8} \cdot(t-5) \end{array} $$
Hier muss nun die Nullstelle gefunden werden:
$$ \begin{array}{l} 0-\frac{245}{24}=-\frac{7}{8} \cdot(t-5) \\ t=\frac{50}{3}=16 \frac{2}{3} \end{array} $$
e) Berechne, um welchen prozentualen Anteil die Immunschwäche den Krankheitsverlauf hinsichtlich aktiver Bläschen verlängert.
Bei nicht Immungeschwächten ist die Krankheit am 12. Tag am Ende.
Bei Immungeschwächten ist sie dagegen erst nach 16 \( \frac{2}{3} \) Tagen zu Ende.
16 \( \frac{2}{3} \)-12=4 \( \frac{2}{3} \)
4 \( \frac{2}{3} \) : 12= x : 100
x=...%