Hi
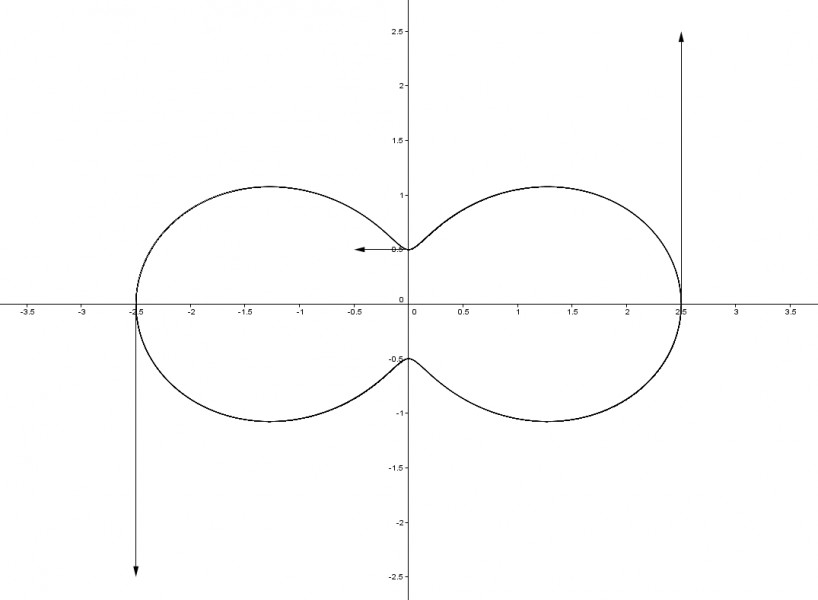
x(t) = (2 cos t, -sin t, 3t)
v = x'(t)
v = (-2 sin t, -cos t, 3)
|v| = sqrt((-2 sin t)^2 + (-cos t)^2 + 9) = sqrt(3 sin^2(t) + 10)
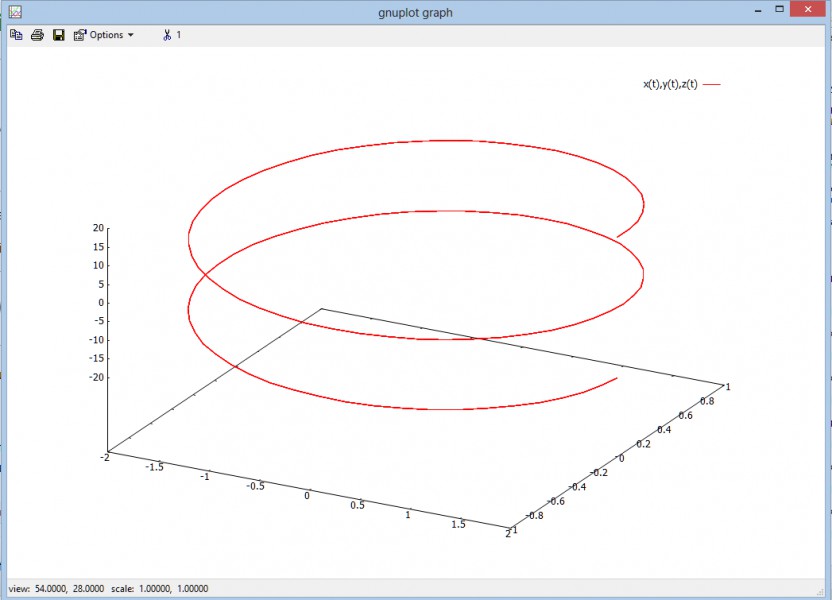
y(t) = ((3/2 + cos(2t))*cos(t), (3/2 + cos(2t))*sin(t))
v = y'(t)
v = (-2 sin(t) - 1.5 sin(3t), cos(t) + 1.5 cos(3t))
|v| = sqrt((-2 sin(t) - 3/2 sin(3 t))^2 + (cos(t) + 3/2 cos(3 t))^2)
y(t = 0) = ((3/2 + cos(0))*cos(0), (3/2 + cos(0))*sin(0))
y(t = 0) = (2.5, 0)
v(t = 0) = (-2 sin(0) - 1.5 sin(0), cos(0) + 1.5 cos(0))
v(t = 0) = (0, 2.5)
|v(t = 0)| = 2.5
y(t = pi/2) = ((3/2 + cos(2*pi/2))*cos(pi/2), (3/2 + cos(2*pi/2))*sin(pi/2))
y(t = pi/2) = (0, 0.5)
v(t = pi/2) = (-2 sin(pi/2) - 1.5 sin(3*pi/2), cos(pi/2) + 1.5 cos(3*pi/2))
v(t = pi/2) = (-0.5, 0)
|v(t = pi/2)| = 0.5
y(t = pi) = ((3/2 + cos(2*pi))*cos(pi), (3/2 + cos(2*pi))*sin(pi))
y(t = pi) = (-2.5, 0)
v(t = pi) = (-2 sin(pi) - 1.5 sin(3*pi), cos(pi) + 1.5 cos(3*pi))
v(t = pi) = (0, -2.5)
|v(t = pi)| = 0.5