Pyramide, Vektoren, Ebenen, Dreieck, Koordinaten

Question

Ich komme bei einer Aufgabe nicht weiter, wie gehe ich hier vor:

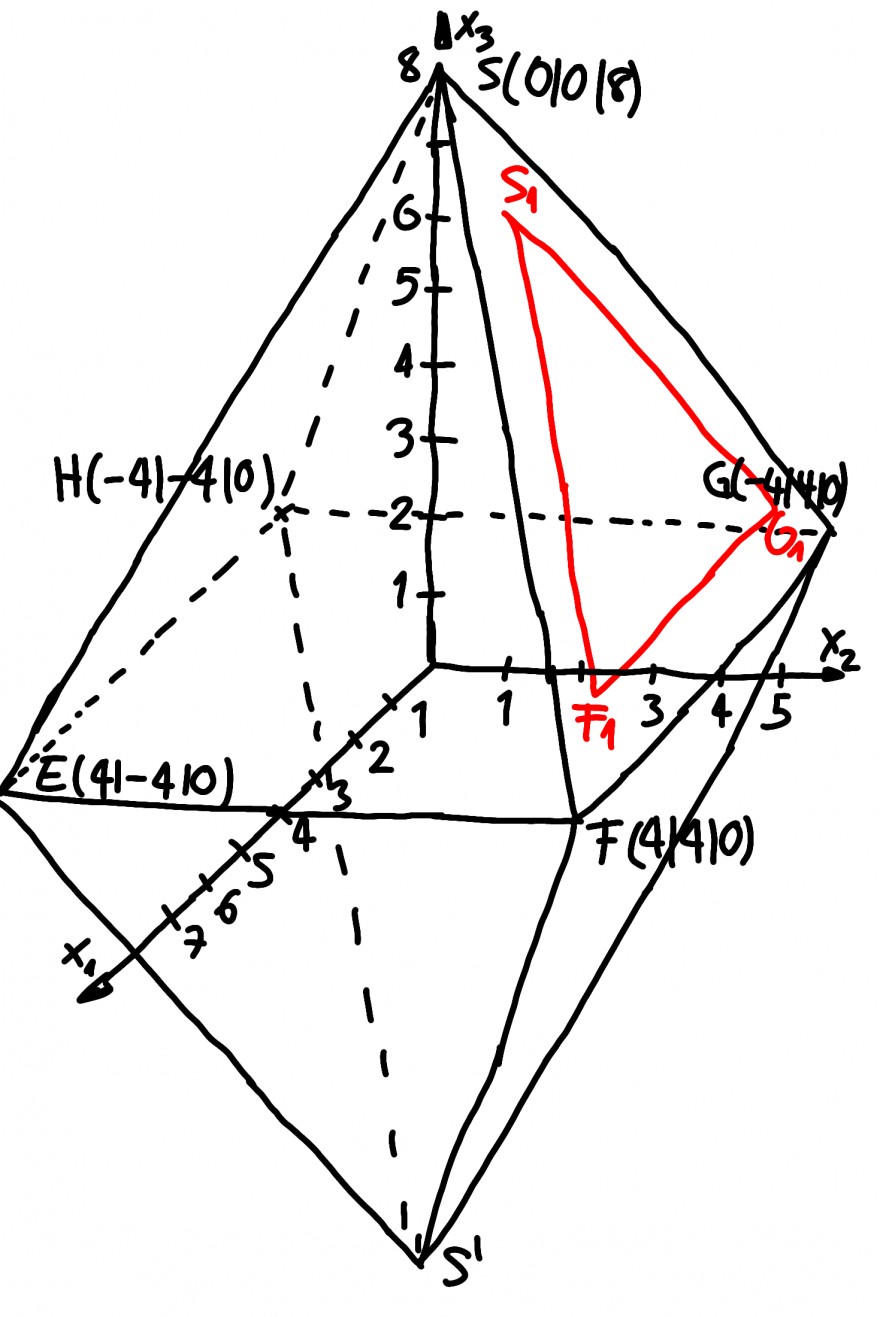
Gegeben ist eine Pyramide mit Spitze S und Grundfläche EFGH.

E(4|-4|0), F(4|4|0), G(-4|4|0), H(-4|-4|0), S(0|0|8)

e) Die Seiten des Dreiecks F_1G1S₁ mit F₁₍2,5|3,5|1) und G₁(-2,5|3,5|1) sind parallel zu den entsprechenden Seiten des Dreiecks FGS. Berechne die Koordinate des Punktes S_1.

und

f) Die Pyramide soll zu einer Doppelpyramide werden. Bestimme die Koordinaten des Punktes S', so dass die Doppelpyramide aus zwei kongruenten Pyramiden besteht.

Könntet ihr mir helfen? Wie gehe ich hier vor?

Answer 1

Hallo,

um S1 herauszufinden, ermittelst du den Schnittpunkt der Gerade durch F1 mit dem Richtungsvektor FS und der durch G1 mit dem Richtungsvektor GS.

S' bestimmst du, indem du S an der Grundfläche der Pyramide spiegelst.

Melde dich bitte, falls du mehr Hilfe brauchst.

Gruß, Silvia

Comments

Achsoo, vielen Dank :)